
题目列表(包括答案和解析)
(本小题满分14分)如图9-3,已知:射线OA为y=kx(k>0,x>0),射线OB为y= -kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k.
(1)当k为定值时,动点P的纵坐标y是横坐标x的函数,求这个函数y=f(x)的解析式;
 (2)根据k的取值范围,确定y=f(x)的定义域.
(2)根据k的取值范围,确定y=f(x)的定义域.
(本小题满分14分)
如图6,正方形ABCD所在平面与圆O所在平面
相交于CD,线段CD为圆O的弦,AE垂直于圆
O所在平面,垂足E是圆O上异于C、D的点,
AE=3,圆O的直径为9.
(1)求证:平面 ABCD ⊥平面 ADE;
(2)求二面角D—BC—E的平面角的正切值.
| 1 | 3 | 5 | 7 | 9 | … |
| 2 | 6 | 10 | 14 | 18 | … |
| 4 | 12 | 20 | 28 | 36 | … |
| 8 | 24 | 40 | 56 | 72 | … |
| 16 | 48 | 80 | 112 | 114 | … |
| … | … | … | … | … | … |
(本小题满分12分)
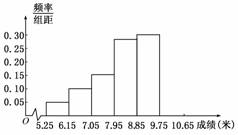
某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30.第6小组的频数是7.
 (1) 求这次铅球测试成绩合格的人数;
(1) 求这次铅球测试成绩合格的人数;
(2) 用此次测试结果估计全市毕业生的情况.若从今年的高中毕业生中随机抽取两名,记![]() 表示两人中成绩不合格的人数,求
表示两人中成绩不合格的人数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(3) 经过多次测试后,甲成绩在8~10米之间,乙成绩在9.5~10.5米之间,现甲、乙各投掷一次,求甲比乙投掷远的概率.
(本大题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
 如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝,再用
如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝,再用![]() 平方米塑料片制成圆柱的侧面和下底面(不安装上底面).
平方米塑料片制成圆柱的侧面和下底面(不安装上底面).
(1)当圆柱底面半径![]() 取何值时,
取何值时,![]() 取得最大值?并求出该
取得最大值?并求出该
最大值(结果精确到0.01平方米);
(2)若要制作一个如图放置的,底面半径为0.3米的灯笼,请作出
用于灯笼的三视图(作图时,不需考虑骨架等因素).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com