
题目列表(包括答案和解析)
|
(本小题满分15分)
已知直线l的方程为: ,直线l与x轴的交点为F,
圆O的方程为:
,直线l与x轴的交点为F,
圆O的方程为: ,
,
C、 D在圆上, CF⊥DF,设线段CD的中点为M.
(1)如果CFDG为平行四边形,求动点G的轨迹;
(2)已知椭圆的中心在原点,右焦点为F,直线l交椭圆于A、B两点,又 ,
,
求椭圆C的方程.
(本题满分15分)已知m是非零实数,抛物线![]() (p>0)
(p>0)
的焦点F在直线![]() 上。
上。
(I)若m=2,求抛物线C的方程
(II)设直线![]() 与抛物线C交于A、B,△A
与抛物线C交于A、B,△A![]() ,△
,△![]() 的重心分别为G,H
的重心分别为G,H
求证:对任意非零实数m,抛物线C的准线与x轴的焦点在以线段GH为直径的圆外。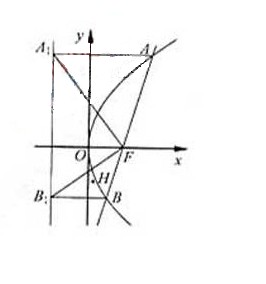
(本小题满分15分)
若函数f(x)=ax3+bx2+cx+d是奇函数,且f(x)极小值=f(-)=-.
(1)求函数f(x)的解析式;
(2)求函数f(x)在[-1,m](m>-1)上的最大值;
(3)设函数g(x)=,若不等式g(x)·g(2k-x)≥(-k)2在(0,2k)上恒成立,求实数k的取值范围.
(本题满分15分) 已知实数a满足1<a≤2,设函数f (x)= x3-
x3- x2+ax.
x2+ax.
(Ⅰ) 当a=2时,求f (x)的极小值;
(Ⅱ) 若函数g(x)=4x3+3bx2-6(b+2)x (b∈R) 的极小值点与f (x)的极小值点相同,
求证:g(x)的极大值小于等于10.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com