
题目列表(包括答案和解析)
(本小题满分15分)
 某旅游商品生产企业,2009年某商品生产的投入成本为1元/件,
某旅游商品生产企业,2009年某商品生产的投入成本为1元/件,
出厂价为流程图的输出结果![]() 元/件,年销售量为10000件,
元/件,年销售量为10000件,
因2010年国家长假的调整,此企业为适应市场需求,
计划提高产品档次,适度增加投入成本.若每件投入成本增加的
比例为![]() (
(![]() ),则出厂价相应提高的比例为
),则出厂价相应提高的比例为![]() ,
,
同时预计销售量增加的比例为![]() .
.
已知得利润![]() (出厂价
(出厂价![]() 投入成本)
投入成本)![]() 年销售量.
年销售量.
(Ⅰ)写出2010年预计的年利润![]()
与投入成本增加的比例![]() 的关系式;
的关系式;
(Ⅱ)为使2010年的年利润比2009年有所增加,
问:投入成本增加的比例![]() 应在什么范围内?
应在什么范围内?
(本小题满分13分) 2010年11月在广州召开亚运会,某小商品公司开发一种亚运会纪念品,每件产品的成本是15元,销售价是20元,月平均销售a件,通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明:如果产品的销售价提高的百分率为x(0<x<1),那么月平均销售量减少的百分率为x2,记改进工艺后,该公司销售纪念品的月平均利润是y(元).
(1)写出y与x的函数关系式;
(2)改进工艺后,确定该纪念品的售价,使该公司销售该纪念品的月平均利润最大.
(本小题满分15分)某生产旅游纪念品的工厂,拟在2010年度将进行系列促销活动.经市场调查和测算,该纪念品的年销售量x万件与年促销费用t万元之间满足3-x与t+1成反比例.若不搞促销活动,纪念品的年销售量只有1万件.已知工厂2010年生产纪念品的固定投资为3万元,每生产1万件纪念品另外需要投资32万元.当工厂把每件纪念品的售价定为:“年平均每件生产成本的150%”与“年平均每![]() 件所占促销费一半”之和时,则当年的产量和销量相等.(利润=收入-生产成本-促销费用)(1)求出x与t所满足的关系式;(2)请把该工厂2010年的年利润y万元表示成促销费t万元的函数;(3)试问:当2010年的促销费投入多少万元时,该工厂的年利润最大?
件所占促销费一半”之和时,则当年的产量和销量相等.(利润=收入-生产成本-促销费用)(1)求出x与t所满足的关系式;(2)请把该工厂2010年的年利润y万元表示成促销费t万元的函数;(3)试问:当2010年的促销费投入多少万元时,该工厂的年利润最大?
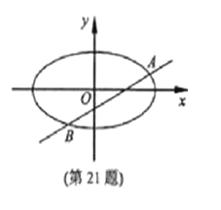 (2010浙江理数)(21) (本题满分15分)已知m>1,直线
(2010浙江理数)(21) (本题满分15分)已知m>1,直线![]() ,椭圆
,椭圆![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点.
的左、右焦点.
(Ⅰ)当直线![]() 过右焦点
过右焦点![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() ,
,![]() 的重心分别为
的重心分别为![]() .若原点
.若原点![]() 在以线段
在以线段![]() 为直径的圆内,求实数
为直径的圆内,求实数![]() 的取值范围.
的取值范围.
(本题满分15分)
国家助学贷款是由财政贴息的信用贷款,旨在帮助高校家庭经济困难学生支付在校学习期间所需的学费、住宿费及生活费.每一年度申请总额不超过6000元.某大学2010届毕业生凌霄在本科期间共申请了![]() 元助学贷款,并承诺在毕业后
元助学贷款,并承诺在毕业后![]() 年内(按
年内(按![]() 个月计)全部还清.签约的单位提供的工资标准为第一年内每月
个月计)全部还清.签约的单位提供的工资标准为第一年内每月![]() 元,第
元,第![]() 个月开始,每月工资比前一个月增加
个月开始,每月工资比前一个月增加![]() 直到
直到![]() 元.凌霄同学计划前
元.凌霄同学计划前![]() 个月每个月还款额为
个月每个月还款额为![]() ,第
,第![]() 个月开始,每月还款额比上一月多
个月开始,每月还款额比上一月多![]() 元.
元.
(1)若凌霄恰好在第36个月(即毕业后三年)还清贷款,求![]() 的值;
的值;
(2)当![]() 时,凌霄同学将在第几个月还清最后一笔贷款?他当月工资的余额是否能满足每月
时,凌霄同学将在第几个月还清最后一笔贷款?他当月工资的余额是否能满足每月![]() 元的基本生活费?
元的基本生活费?
(参考数据:![]() )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com