
题目列表(包括答案和解析)
求曲线y=x2+1在点P(1,2)处的切线的斜率k.
探究:用导数的方法求P点的切线的斜率:在P点附近作另一个点Q,先表示出割线PQ的斜率,让后将Q点无限接近于P点,即当Δx趋向于0时,割线PQ的斜率为过P点的切线的斜率.
| ) | φ(x) |
| ) | φ(x) |
| y′ |
| y |
| f′(x) |
| f(x) |
| ) | φ(x) |
| f′(x) |
| f(x) |
| x | x |
| y′ |
| y |
| f′(x) |
| f(x) |
| f′(x) |
| f(x) |
| 1 |
| x |
我们把形如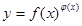 的函数称为幂指函数,幂指函数在求导时,可以利用对数:在函数解析式两边求对数得
的函数称为幂指函数,幂指函数在求导时,可以利用对数:在函数解析式两边求对数得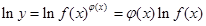 ,两边对
,两边对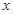 求导数,得
求导数,得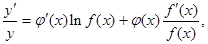 于是
于是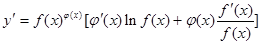 ,运用此方法可以求得函数
,运用此方法可以求得函数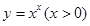 在(1,1)处的切线方程是 _________
在(1,1)处的切线方程是 _________
已知函数f(x)=alnx+bx,且f(1)= -1,f′(1)=0,
⑴求f(x);
⑵求f(x)的最大值;
⑶若x>0,y>0,证明:lnx+lny≤![]() .
.
本题主要考查函数、导数的基本知识、函数性质的处理以及不等式的综合问题,同时考查考生用函数放缩的方法证明不等式的能力.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com