①
②
①×3,得 6x+3y=15. ③
②+③,得 7x=21,
x=3. …………………………3′
把x=3代入①,得2×3+y=5,
y=-1.
∴原方程组的解是 ………………………………6′
………………………………6′
17.(本小题满分6分)
解:⑴ 正确补全频数分布直方图;
………………………………2′
⑵ 样本的中位数在155~160cm的范围内; ………………………………4′
⑶ 八年级. ………………………………6′
18.(本小题满分6分)
解:⑴  (元); …………………………4′
(元); …………………………4′
⑵ ∵11.875元>10元,
∴选择转转盘.
……………………………6′
(如果学生选择直接获得购物券,只要回答合理即可同样得分)
19.(本小题满分6分)
 解:过C作AB的垂线,交直线AB于点D,得到Rt△ACD与Rt△BCD.
解:过C作AB的垂线,交直线AB于点D,得到Rt△ACD与Rt△BCD.
设BD=x海里,
在Rt△BCD中,tan∠CBD= ,
,
∴CD=x ?tan63.5°.
在Rt△ACD中,AD=AB+BD=(60+x)海里,tan∠A= ,
,
∴CD=( 60+x ) ?tan21.3°.
……………………………4′
∴x?tan63.5°=(60+x)?tan21.3°,即  .
.
解得,x=15.
答:轮船继续向东航行15海里,距离小岛C最近. …………………………6′
20.(本小题满分8分)
 解:⑴ 设生产A种饮料x瓶,根据题意得:
解:⑴ 设生产A种饮料x瓶,根据题意得:
解这个不等式组,得20≤x≤40.
因为其中正整数解共有21个,
所以符合题意的生产方案有21种.
……………………………4′
⑵ 根据题意,得 y=2.6x+2.8(100-x).
整理,得 y=-0.2x+280. ……………………………6′
∵k=-0.2<0,
∴y随x的增大而减小.
∴当x=40时成本总额最低. …………………………8′
21.(本小题满分8分)
 证明:⑴ 由折叠可知:∠D=∠D′,CD=AD′,∠C=∠D′AE.
证明:⑴ 由折叠可知:∠D=∠D′,CD=AD′,∠C=∠D′AE.
∵四边形ABCD是平行四边形,
∴∠B=∠D,AB=CD,∠C=∠BAD.………2′
∴∠B=∠D′,AB=AD′,
∠D′AE=∠BAD,即∠1+∠2=∠2+∠3.
∴∠1=∠3.
∴△ABE ≌△A D′F. ……………4′
⑵ 四边形AECF是菱形.
由折叠可知:AE=EC,∠4=∠5.
∵四边形ABCD是平行四边形,∴AD∥BC.
∴∠5=∠6.∴∠4=∠6.∴AF=AE.
∵AE=EC, ∴AF=EC.
又∵AF∥EC,
∴四边形AECF是平行四边形.
∵AF=AE,
∴四边形AECF是菱形.
……………………………8′
22.(本小题满分10分)
解:⑴ y=(x-50)∙ w
=(x-50) ∙ (-2x+240)
=-2x2+340x-12000,
∴y与x的关系式为:y=-2x2+340x-12000. ……………………3′
⑵ y=-2x2+340x-12000
=-2 (x-85) 2+2450,
∴当x=85时,y的值最大.
………………………6′
⑶ 当y=2250时,可得方程 -2 (x-85 )2 +2450=2250.
解这个方程,得 x1=75,x2=95. ………………………8′
根据题意,x2=95不合题意应舍去.
 ∴当销售单价为75元时,可获得销售利润2250元. …………………10′
∴当销售单价为75元时,可获得销售利润2250元. …………………10′
23.(本小题满分10分)
解:⑵ ∵AP= AD,△ABP和△ABD的高相等,
AD,△ABP和△ABD的高相等,
∴S△ABP= S△ABD .
S△ABD .
又∵PD=AD-AP= AD,△CDP和△CDA的高相等,
AD,△CDP和△CDA的高相等,
∴S△CDP= S△CDA .
S△CDA .
∴S△PBC =S四边形ABCD-S△ABP-S△CDP
=S四边形ABCD- S△ABD-
S△ABD- S△CDA
S△CDA
=S四边形ABCD- (S四边形ABCD-S△DBC)-
(S四边形ABCD-S△DBC)- (S四边形ABCD-S△ABC)
(S四边形ABCD-S△ABC)
= S△DBC+
S△DBC+ S△ABC .
S△ABC .
∴S△PBC= S△DBC+
S△DBC+ S△ABC .
……………………………4′
S△ABC .
……………………………4′
⑶ S△PBC= S△DBC+
S△DBC+ S△ABC ;
……………………………5′
S△ABC ;
……………………………5′
⑷ S△PBC= S△DBC+
S△DBC+ S△ABC ;
S△ABC ;
∵AP= AD,△ABP和△ABD的高相等,
AD,△ABP和△ABD的高相等,
∴S△ABP= S△ABD .
S△ABD .
又∵PD=AD-AP= AD,△CDP和△CDA的高相等,
AD,△CDP和△CDA的高相等,
∴S△CDP= S△CDA .
S△CDA .
∴S△PBC =S四边形ABCD-S△ABP-S△CDP
=S四边形ABCD- S△ABD-
S△ABD- S△CDA
S△CDA
=S四边形ABCD- (S四边形ABCD-S△DBC)-
(S四边形ABCD-S△DBC)- (S四边形ABCD-S△ABC)
(S四边形ABCD-S△ABC)
= S△DBC+
S△DBC+ S△ABC .
S△ABC .
∴S△PBC= S△DBC+
S△DBC+ S△ABC . ……………………………8′
S△ABC . ……………………………8′
问题解决: S△PBC= S△DBC+
S△DBC+ S△ABC . ……………………………10′
S△ABC . ……………………………10′
24.(本小题满分12分)
解:⑴ 根据题意:AP=t cm,BQ=t cm.
△ABC中,AB=BC=3cm,∠B=60°,
∴BP=(3-t ) cm.
△PBQ中,BP=3-t,BQ=t,
若△PBQ是直角三角形,则∠BQP=90°或∠BPQ=90°.
 当∠BQP=90°时,BQ=
当∠BQP=90°时,BQ= BP.
BP.
即t= (3-t ),
(3-t ),
t=1 (秒).
当∠BPQ=90°时,BP= BQ.
BQ.
3-t= t,
t,
t=2 (秒).
答:当t=1秒或t=2秒时,△PBQ是直角三角形. …………………4′
⑵ 过P作PM⊥BC于M .
Rt△BPM中,sin∠B= ,
,
∴PM=PB?sin∠B= (3-t ).
(3-t ).
∴S△PBQ= BQ?PM=
BQ?PM= ? t ?
? t ? (3-t ).
(3-t ).
∴y=S△ABC-S△PBQ
= ×32×
×32× -
- ? t ?
? t ? (3-t )
(3-t )
= .
.
∴y与t的关系式为: y= . …………………6′
. …………………6′
假设存在某一时刻t,使得四边形APQC的面积是△ABC面积的 ,
,
则S四边形APQC= S△ABC .
S△ABC .
∴ =
= ×
× ×32×
×32× .
.
∴t 2-3 t+3=0.
∵(-3) 2-4×1×3<0,
∴方程无解.
∴无论t取何值,四边形APQC的面积都不可能是△ABC面积的 .……8′
.……8′
⑶ 在Rt△PQM中,
MQ= =
= .
.
MQ 2+PM 2=PQ 2.
∴x2=[ (1-t ) ]2+[
(1-t ) ]2+[ (3-t ) ]2
(3-t ) ]2
=
= =3t2-9t+9.
……………………………10′
=3t2-9t+9.
……………………………10′
∴t2-3t= .
.
∵y= ,
,
∴y= =
= =
= .
.
∴y与x的关系式为:y= . ……………………………12′
. ……………………………12′

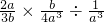 =________.
=________.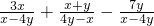 =________.
=________.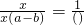 .________.
.________.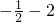 =________.
=________. =________.
=________. ________.
________. ________.
________. _________.
_________. =_________.
=_________.
