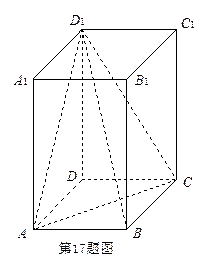17. 在长方体中.底面是边长为2的正方形. .的中点. 在上.且. (Ⅰ)求证:平面, (Ⅱ)求三棱锥的体积. (Ⅰ)证明:设BD交AC于O.连结. . 又. ∴∥. ∴∥平面. (Ⅱ)解:. 18. 设公比大于零的等比数列的前n项和为.且.. (Ⅰ)求数列的通项公式, (Ⅱ)设.求. 19. 如下图.从参加数学竞赛的学生中抽出60名.将其成绩整理后画出的频率分布直方图如下. 观察图形.回答下列问题: (Ⅰ)79.5-89.5这一组的频数.频率分别是多少? (Ⅱ)估计这次数学竞赛的平均成绩是多少? (Ⅲ)估计这次数学竞赛的及格率. 解:(Ⅰ)频率为0.025 × 10 = 0.25.频数为60 × 0.25 = 15. (Ⅱ)平均成绩为 . (Ⅲ)0.015 × 10 + 0.03 × 10 + 0.025 × 10 + 0.005 × 10 = 0.75. 20. 袋中有大小.形状相同的白.黑球各一个.现有放回地随机摸取3次.每次摸取一个球. (Ⅰ)试问:一共有多少种不同的结果?请列出所有可能的结果, (Ⅱ)若摸到白球时得1分.摸到黑球时得2分.求3次摸球所得总分大于4分的概率. 21. 在中.... (Ⅰ)求的值, (Ⅱ)求的值. 解:(Ⅰ)因为.根据正弦定理知..即, (Ⅱ)利用余弦定理的推论得.易得. 因此.. 所以. 22. 已知圆与直线相切于点.且圆心在直线上. (Ⅰ)求圆的方程, (Ⅱ)设直线与圆相交于两点.是坐标原点.求的面积最大值.并求取得最大值时直线的方程. 解:(Ⅰ). (Ⅱ)... . 由. 设.则. . 当.即.时.. ∴S的最大值为2.取得最大值时.所求直线. 另解: . 当且仅当即时.. 【
查看更多】
题目列表(包括答案和解析)
(本小题满分8分)
在长方体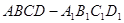 中,底面是边长为2的正方形,
中,底面是边长为2的正方形, .
.
(Ⅰ)指出二面角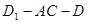 的平面角,并求出它的正切值;
的平面角,并求出它的正切值;
(Ⅱ)求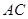 与
与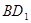 所成的角.
所成的角.
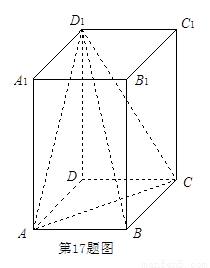
查看答案和解析>>
(本小题满分8分)
在长方体
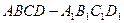
中,底面是边长为2的正方形,
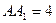
.
(Ⅰ)指出二面角
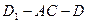
的平面角,并求出它的正切值;
(Ⅱ)求
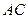
与
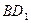
所成的角.
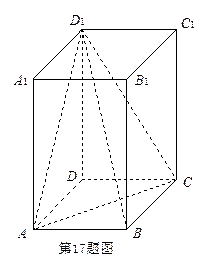
查看答案和解析>>

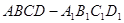 中,底面是边长为2的正方形,
中,底面是边长为2的正方形, .
.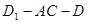 的平面角,并求出它的正切值;
的平面角,并求出它的正切值;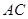 与
与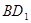 所成的角.
所成的角.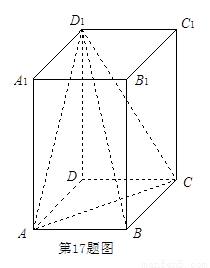
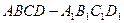 中,底面是边长为2的正方形,
中,底面是边长为2的正方形,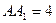 .
.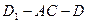 的平面角,并求出它的正切值;
的平面角,并求出它的正切值;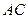 与
与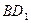 所成的角.
所成的角.