
题目列表(包括答案和解析)
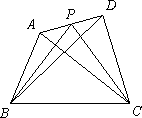
提出问题:如图,在四边形ABCD中,P是AD边上任意一点,△PBC与△ABC和△DBC的面积之间有什么关系?

探究发现:为了解决这个问题,我们可以先从一些简单的、特殊的情形入手:
(1)当AP=![]() AD时(如图):
AD时(如图):
∵AP=![]() AD,△ABP和△ABD的高相等,
AD,△ABP和△ABD的高相等,
∴S△ABP=![]() S△ABD.
S△ABD.
∵PD=AD-AP=![]() AD,△CDP和△CDA的高相等,
AD,△CDP和△CDA的高相等,
∴S△CDP=![]() S△CDA.
S△CDA.
∴S△PBC=S四边形ABCD-S△ABP-S△CDP
=S四边形ABCD-![]() S△ABD-
S△ABD-![]() S△CDA
S△CDA
=S四边形ABCD-![]() (S四边形ABCD-S△DBC)-
(S四边形ABCD-S△DBC)-![]() (S四边形ABCD-S△ABC)
(S四边形ABCD-S△ABC)
=![]() S△DBC+
S△DBC+![]() S△ABC.
S△ABC.
(2)当![]() 时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
(3)当![]() 时,S△PBC与S△ABC和S△DBC之间的关系式为:________;
时,S△PBC与S△ABC和S△DBC之间的关系式为:________;
(4)一般地,当![]() (n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
问题解决:当![]() 时,S△PBC与S△ABC和S△DBC之间的关系式为:________.
时,S△PBC与S△ABC和S△DBC之间的关系式为:________.
提出问题:如图①,在四边形ABCD中,P是AD边上任意一点,△PBC与△ABC和△DBC的面积之间有什么关系?
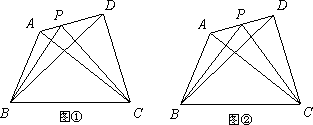
探究发现:为了解决这个问题,我们可以先从一些简单的、特殊的情形入手:
(1)当AP=![]() AD时(如图②):
AD时(如图②):
∵AP=![]() AD,△ABP和△ABD的高相等,
AD,△ABP和△ABD的高相等,
∴S△ABP=![]() S△ABD.
S△ABD.
∵PD=AD-AP=![]() AD,△CDP和△CDA的高相等,
AD,△CDP和△CDA的高相等,
∴S△CDP=![]() S△CDA.
S△CDA.
∴S△PBC=S四边形ABCD-S△ABP-S△CDP
=S四边形ABCD-![]() S△ABD-
S△ABD-![]() S△CDA
S△CDA
=S四边形ABCD-![]() (S四边形ABCD-S△DBC)-
(S四边形ABCD-S△DBC)-![]() (S四边形ABCD-S△ABC)
(S四边形ABCD-S△ABC)
=![]() S△DBC+
S△DBC+![]() S△ABC.
S△ABC.
(2)当AP=![]() AD时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
AD时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
(3)当AP=![]() AD时,S△PBC与S△ABC和S△DBC之间的关系式为:________;
AD时,S△PBC与S△ABC和S△DBC之间的关系式为:________;
(4)一般地,当AP=![]() AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
问题解决:当AP=![]() AD(0≤
AD(0≤![]() ≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为:________.
≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为:________.
提出问题:如图①,在四边形ABCD中,P是AD边上任意一点,△PBC与△ABC和△DBC的面积之间有什么关系?
探究发现:为了解决这个问题,我们可以先从一些简单的、特殊的情形入手:
 (1)当AP=
(1)当AP=![]() AD时(如图②):
AD时(如图②):
∵AP=![]() AD,△ABP和△ABD的高相等,
AD,△ABP和△ABD的高相等,
∴S△ABP=![]() S△ABD .
S△ABD .
∵PD=AD-AP=![]() AD,△CDP和△CDA的高相等,
AD,△CDP和△CDA的高相等,
 ∴S△CDP=
∴S△CDP=![]() S△CDA .
S△CDA .
∴S△PBC =S四边形ABCD-S△ABP-S△CDP
=S四边形ABCD-![]() S△ABD-
S△ABD-![]() S△CDA
S△CDA
=S四边形ABCD-![]() (S四边形ABCD-S△DBC)-
(S四边形ABCD-S△DBC)-![]() (S四边形ABCD-S△ABC)
(S四边形ABCD-S△ABC)
=![]() S△DBC+
S△DBC+![]() S△ABC .
S△ABC .
(2)当AP=![]() AD时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
AD时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
(3)当AP=![]() AD时,S△PBC与S△ABC和S△DBC之间的关系式为:________________;
AD时,S△PBC与S△ABC和S△DBC之间的关系式为:________________;
(4)一般地,当AP=![]() AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
问题解决:当AP=![]() AD(0≤
AD(0≤![]() ≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为:___________.
≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为:___________.
提出问题:如图①,在四边形ABCD中,P是AD边上任意一点,△PBC与△ABC和△DBC的面积之间有什么关系?
探究发现:为了解决这个问题,我们可以先从一些简单的、特殊的情形入手:
(1
)当AP=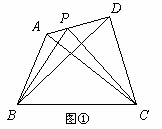

∵AP=![]() AD,△ABP和△ABD的高相等,
AD,△ABP和△ABD的高相等,
∴S△ABP=![]() S△ABD .
S△ABD .
∵PD=AD-AP=![]() AD,△CDP和△CDA的高相等,
AD,△CDP和△CDA的高相等,
∴S△CDP=![]() S△CDA .
S△CDA .
∴S△PBC =S四边形ABCD-S△ABP-S△CDP
=S四边形ABCD-![]() S△ABD-
S△ABD-![]() S△CDA
S△CDA
=S四边形ABCD-![]() (S四边形ABCD-S△DBC)-
(S四边形ABCD-S△DBC)-![]() (S四边形ABCD-S△ABC)
(S四边形ABCD-S△ABC)
=![]() S△DBC+
S△DBC+![]() S△ABC .
S△ABC .
(2
)当AP=(3
)当AP=(4
)一般地,当AP=问题解决:当AP=![]() AD(0≤
AD(0≤![]() ≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为:___________.
≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为:___________.
说明:
1.如果考生的解法与本解法不同,可参照本评分标准制定相应评分细则.
2.当考生的解答在某一步出现错误,影响了后继部分时,如果这一步以后的解答未改变这道题的内容和难度,可视影响程度决定后面部分的给分,但不得超过后面部分应给分数的一半;如果这一步以后的解答有较严重的错误,就不给分.
3.为阅卷方便,本解答中的推算步骤写得较为详细,但允许考生在解答过程中,合理省略非关键性的推算步骤.
4.解答右端所注分数,表示考生正确做到这一步应得的累加分数.
一、选择题(本题满分21分,共有7道小题,每小题3分)
题号
1
2
3
4
5
6
7
答案
D
B
A
C
D
A
C
二、填空题(本题满分21分,共有7道小题,每小题3分)
题号
8
9
10
11
答案
1
甲


题号
12
13
14
答案
16
(8,3)
4
32
三、作图题(本题满分6分)
15.⑴ 正确作出图形,并做答. …………………………3′
⑵ 132 . …………………………6′
四、解答题(本题满分72分,共有9道小题)
16.(本小题满分6分)
|