
题目列表(包括答案和解析)
在古希腊毕达哥拉斯学派把1,3,6,10,15,21,28,……这些数叫做三角形数,因为这些数对应的点可以排成一个正三角形(如下图所示)则第n个三角形数为( )

A.n B.n(n+1)
C.n2-1 D.n(n-1)
在古希腊毕达哥拉斯学派把1,3,6,10,15,21,28,……这些数叫做三角形数,因为这些数对应的点可以排成一个正三角形(如下图所示)则第n个三角形数为( )
| A.n | B.n(n+1) |
| C.n2-1 | D.n(n-1) |
| n(n+1) |
| 2 |
| n(n+1)(n+2) |
| 6 |
| 0+2+6 |
| 4 |
| 2(1+3) |
| 4 |
| 0+3+9+18 |
| 9 |
| 3(1+3+6) |
| 9 |
| 10 |
| 3 |
| an |
| an+1 |
| an+1 |
| an |
 ,前n项和为
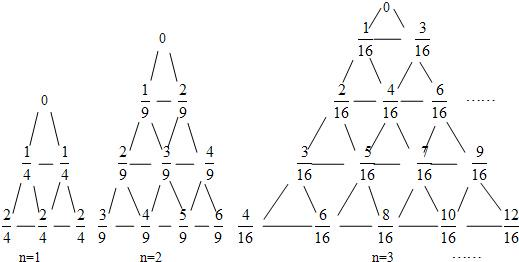
,前n项和为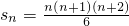 ,如下图所示,有一列三角形数表,其位于三角形的三边及平行于某边的任一直线上的数(当数的个数不少于3时)都分别依次成等差数列,依次记各三角形数表中的所有数之和为an,则
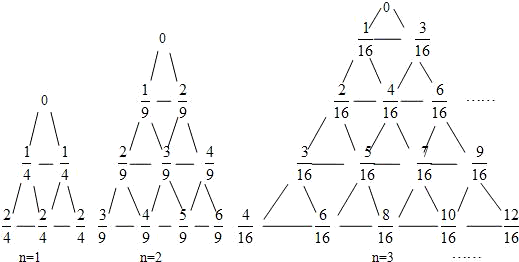
,如下图所示,有一列三角形数表,其位于三角形的三边及平行于某边的任一直线上的数(当数的个数不少于3时)都分别依次成等差数列,依次记各三角形数表中的所有数之和为an,则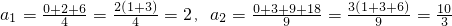 .
.
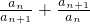 ,证明2n<b1+b2+b3+…+bn<2n+2(n∈N*).
,证明2n<b1+b2+b3+…+bn<2n+2(n∈N*). ,前n项和为
,前n项和为 ,如下图所示,有一列三角形数表,其位于三角形的三边及平行于某边的任一直线上的数(当数的个数不少于3时)都分别依次成等差数列,依次记各三角形数表中的所有数之和为an,则
,如下图所示,有一列三角形数表,其位于三角形的三边及平行于某边的任一直线上的数(当数的个数不少于3时)都分别依次成等差数列,依次记各三角形数表中的所有数之和为an,则 .
.
 ,证明2n<b1+b2+b3+…+bn<2n+2(n∈N*).
,证明2n<b1+b2+b3+…+bn<2n+2(n∈N*).湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com