等差数列 (1)定义.{an}为等差数列an+1-an=d.n∈N+2an=an-1+an+1(n≥2.n∈N+), (2)通项公式:an=an+(n-1)d.an=am+(n-m)d, 前n项和公式:, (3)性质:an=an+b.即an是n的一次型函数.系数a为等差数列的公差, Sn=an2+bn.即Sn是n的不含常数项的二次函数, 若{an}.{bn}均为等差数列.则{an±nn},{},{kan+c}均为等差数列, 当m+n=p+q时.am+an=ap+aq.特例:a1+an=a2+an-1=a3+an-2=-,当2n=p+q时.2an=ap+aq, 当n为奇数时.S2n-1=an,S奇=a中.S偶=a中. 【
查看更多】
题目列表(包括答案和解析)
等差数列{b
n}的首项为1,公差为2,数列{a
n}与{b
n}且满足关系式
bn=| a1+2a2+3a3+…+nan |
| 1+2+3+…+n |
(n∈N
*),奇函数f(x)定义域为R,当x<0时,
f(x)=-.
(1)求函数f(x)的解析式;
(2)求数列{a
n}的通项公式;
(3)若q>0,且
f(an)=0,求证p+q>2.
查看答案和解析>>
等差数列{b
n}的首项为1,公差为2,数列{a
n}与{b
n}且满足关系式

(n∈N
*),奇函数f(x)定义域为R,当x<0时,
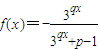
.
(1)求函数f(x)的解析式;
(2)求数列{a
n}的通项公式;
(3)若
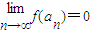
,求p+q必须满足的条件.
查看答案和解析>>
等差数列{b
n}的首项为1,公差为2,数列{a
n}与{b
n}且满足关系式

(n∈N
*),奇函数f(x)定义域为R,当x<0时,
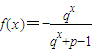
.
(1)求函数f(x)的解析式;
(2)求数列{a
n}的通项公式;
(3)若q>0,且
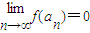
,求证p+q>2.
查看答案和解析>>
等差数列{b
n}的首项为1,公差为2,数列{a
n}与{b
n}且满足关系式
bn=| a1+2a2+3a3+…+nan |
| 1+2+3+…+n |
(n∈N
*),奇函数f(x)定义域为R,当x<0时,
f(x)=-.
(1)求函数f(x)的解析式;
(2)求数列{a
n}的通项公式;
(3)若q>0,且
f(an)=0,求证p+q>2.
查看答案和解析>>
已知等差数列{a
n}前n项和为S
n,且a
2=5,S
10=120.
(1)求数列{a
n}的通项公式;
(2)定义:称
为n个正数p
1,p
2,…p
n的“权倒数”.若数列{b
n}的前n项的“权倒数”为
,求数列{b
n}的通项公式.
查看答案和解析>>

 (n∈N*),奇函数f(x)定义域为R,当x<0时,
(n∈N*),奇函数f(x)定义域为R,当x<0时,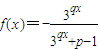 .
.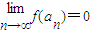 ,求p+q必须满足的条件.
,求p+q必须满足的条件. (n∈N*),奇函数f(x)定义域为R,当x<0时,
(n∈N*),奇函数f(x)定义域为R,当x<0时,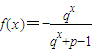 .
.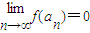 ,求证p+q>2.
,求证p+q>2.