
题目列表(包括答案和解析)
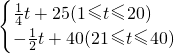 (t
(t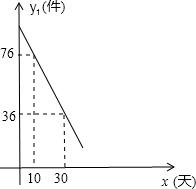 为整数);
为整数);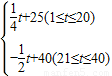 (t为整数);
(t为整数);
 (t为整数);
(t为整数);
|
 为整数);
为整数);| 时间t(天) | 1 | 3 | 6 | … |
| 日销售量m(件) | 78 | 74 | 68 | … |
说明:若有本参考答案没有提及的解法,只要解答正确,请参照给分.
第I卷(选择题 共24分)
一、选择题(本大题共8题,每题3分,共24分)
1.B 2.C 3.C 4.B 5.D 6.C 7.A 8.B
第II卷(非选择题 共126分)
二、填空题:(每题3分,共30分)
9. ; 10.
; 10. ; 11.
; 11. ; 12.
; 12. ; 13.抽样调查
; 13.抽样调查
14.范; 15. ; 16.60; 17.
; 16.60; 17. ; 18.8
; 18.8
说明:第11题若答案是 不给分;第17题若答案是
不给分;第17题若答案是 给2分.
给2分.
三、解答题:(本大题共8题,共96分)
19.(1)解:原式
 .
.
说明:第一步中每对一个运算给1分,第二步2分.
(2)解:原式


 .
.
20.解:(1)15 5.5 6 1.8 .
(2)①平均数或中位数或众数;
②平均数不能较好地反映乙队游客的年龄特征.
因为乙队游客年龄中含有两个极端值,受两个极端值的影响,导致乙队游客年龄方差较大,平均数高于大部分成员的年龄.
说明:第(1)题中平均数、中位数、众数各1分,方差2分,第(2)题中学生说理只要说出受“极端值影响”的大意即可给分.
21.解:(1) 的数量关系是
的数量关系是 .
.
理由如下: .
.
又 ,
,
 (SAS).
(SAS).
 .
.
(2)线段 是线段
是线段 和
和 的比例中项.
的比例中项.
理由如下: ,
, .
.
 .
.
又 ,
,
 .
.
 .
.
即线段 是线段
是线段 和
和 的比例中项.
的比例中项.
说明:若第(1)、(2)题中结论已证出,但在证明前未作判断的不扣分.
22.解:(1)不同意小明的说法.
因为摸出白球的概率是 ,摸出红球的概率是
,摸出红球的概率是 ,
,
因此摸出白球和摸出红球不是等可能的.
(2)树状图如图(列表略)


 (两个球都是白球)
(两个球都是白球)
(3)(法一)设应添加 个红球,
个红球,
由题意得
解得 (经检验是原方程的解)
(经检验是原方程的解)
答:应添加3个红球.
(法二) 添加后
添加后 (摸出红球)
(摸出红球)
 添加后
添加后 (摸出白球)
(摸出白球)
 添加后球的总个数
添加后球的总个数 .
.
 应添加
应添加 个红球.
个红球.
23.解:(1)设该校采购了 顶小帐篷,
顶小帐篷, 顶大帐篷.
顶大帐篷.
根据题意,得
解这个方程组,得
(2)设甲型卡车安排了 辆,则乙型卡车安排了
辆,则乙型卡车安排了 辆.
辆.
根据题意,得
解这个不等式组,得 .
.
 车辆数
车辆数 为正整数,
为正整数,
 或16或17.
或16或17.
 或4或3.
或4或3.
答:(1)该校采购了100顶小帐篷,200顶大帐篷.
(2)安排方案有:①甲型卡车15辆,乙型卡车5辆;②甲型卡车16辆,乙型卡车4辆;③甲型卡车17辆,乙型卡车3辆.
24.解:(1) 所在直线与小圆相切,
所在直线与小圆相切,
理由如下:过圆心 作
作 ,垂足为
,垂足为 ,
,

 是小圆的切线,
是小圆的切线, 经过圆心
经过圆心 ,
,
 ,又
,又
 平分
平分 .
.
 .
.
 所在直线是小圆的切线.
所在直线是小圆的切线.
(2)
理由如下:连接 .
.
 切小圆
切小圆 于点
于点 ,
, 切小圆
切小圆 于点
于点 ,
,
 .
.
 在
在 与
与 中,
中,
 ,
,
 (HL)
(HL)  .
.
 ,
, .
.
(3) ,
, .
.
 ,
, .
.
 圆环的面积
圆环的面积
又 ,
,  .
.
说明:若第(1)、(2)题中结论已证出,但在证明前未作判断的不扣分.
25.解:(1)将 和
和 代入一次函数
代入一次函数 中,有
中,有 .
.

 .
.
经检验,其它点的坐标均适合以上解析式,
故所求函数解析式为 .
.
(2)设前20天日销售利润为 元,后20天日销售利润为
元,后20天日销售利润为 元.
元.
由 ,
,
 ,
, 当
当 时,
时, 有最大值578(元).
有最大值578(元).
由 .
.
 且对称轴为
且对称轴为 ,
, 函数
函数 在
在 上随
上随 的增大而减小.
的增大而减小.
 当
当 时,
时, 有最大值为
有最大值为 (元).
(元).
 ,故第14天时,销售利润最大,为578元.
,故第14天时,销售利润最大,为578元.
(3)
对称轴为 .
.

 ,
, 当
当 即
即 时,
时, 随
随 的增大而增大.
的增大而增大.
又 ,
, .
.
26.解:(1) 在矩形
在矩形 中,
中, ,
,


 ,
,
 .
.
 .
.
(2)(法一)
 ,易得
,易得 ,
, .
.
 .
.
 梯形面积
梯形面积 .
.
 .
.
 ,
, .(负值舍去,经检验是原方程的解)
.(负值舍去,经检验是原方程的解)
(法二) 由(1)得
由(1)得 .
.
 ,易得
,易得 ,
, .
.
 ,
, ,
,
 ,
,
 .(负值舍去,经检验是原方程的解)
.(负值舍去,经检验是原方程的解)
(3)(法一)与(1)、(2)同理得 ,
,
 .
.
 直线
直线 过点
过点 .
. .
.
 .(负值舍去,经检验是原方程的解)
.(负值舍去,经检验是原方程的解)
(法二)连接 交
交 于点
于点 ,则
,则 .
.
又 ,
, .
.

 .
. 是等边三角形,
是等边三角形,
 .
.
(4)(法一)在 中,
中, ,
, ,
, ,
,
由 有:
有: ,
, .
.
 ,
, .
.
 ,又
,又 ,
, .
.

 ,
,
 与
与 的函数关系式是
的函数关系式是 ,
, .
.
(法二)在 中,
中, .
.
由 ,有
,有 .
.
 ,
, ,
,
 ,又
,又 .
.
 ,
, ,
,
 .
.
 与
与 的函数关系式是
的函数关系式是 ,
, .
.
说明:写出 和
和 各得1分.
各得1分.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com