练习册

  • 练习册
  • 试题
    已知1<m<n.m.n∈N*.求证:(1+m)n>(1+n)m. 证法一:由二项式定理(1+m)n=Cm0+Cm1+-+Cmn. (1+n)m=Cn0+Cn1+-+C. 又因为C=.C=. 而Ami>A.所以Cm2>C.C>Cn3.-.C>C. 又因为C=C.C=C. 所以(1+m)n>(1+n)m. 证法二:(1+m)n>(1+n)mnln(1+m)>mln(1+n) >. 令f(x)=.x∈［2.+∞］. 只要证f(x)在［2.+∞］上单调递减.只要证f ′(x)<0. f ′(x)==. 当x≥2时.x-lg(1+x)<0. x2(1+x)>0.得f ′(x)<0.即x∈［2,+∞］时.f ′(x)<0. 以上各步都可逆推.得(1+m)n>(1+n)m. [探索题]已知数列是首项是a1.公比为q的等比数列. (1)求和: 的结果归纳概括出关于正整数n的一个结论.并加以证明. (3)设q≠1.Sn是等比数列的前n项和.求: . 解:(1) (2)归纳概括的结论为: 若数列是首项为a1.公比为q的等比数列.则 (3)因为 【查看更多】

     

    题目列表(包括答案和解析)

    已知O<m<l<n，关于x的不等式O<mx-nx<1的解集是{x|-l<x<O}，则m，n满足的关系是    (  )

      A、     B、

      C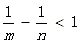．    D、m，n的关系不能确定

     

    查看答案和解析>>

    （08年南昌市一模理）（12分）已知函数f (x) =lnx,g(x) =，（a为常数），若直线l与y =f(x), y =g(x)的图象都相切，且l与y = f(x)的图象相切的切点的横坐标为1.

    （1）求直线l的方程及a的值；

    （2） 当 2 ≤m <时,求h(x)= f(x)―f(x)[2g(x)- m +1]在[,2]上的最大值.

    查看答案和解析>>

    （09年临沂一模理）（12分）

    已知点M在椭圆（a>b>0）上，以M为圆心的圆与x轴相切于椭圆的右焦点F。

    (1)若圆M与y轴相交于A、B两点，且△ABM是边长为2的正三角形，求椭圆的方程;

    (2)若点F（1,0），设过点F的直线l交椭圆于C、D两点，若直线l绕点F任意转动时恒有|OC|2+|OD|2<|CD|2，求a的取值范围。

    查看答案和解析>>

    （1）（本小题满分7分）

    选修4-4：矩阵与变换

    已知矩阵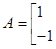 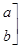 ,A的一个特征值，其对应的特征向量是.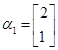

    （Ⅰ）求矩阵；

    （Ⅱ）求直线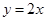在矩阵M所对应的线性变换下的像的方程

     

     

    （2）

    （本小题满分7分）选修4-4：坐标系与参数方程

    已知曲线C的极坐标方程是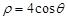．以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线l的参数方程是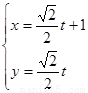：，求直线l与曲线C相交所成的弦的弦长．

    （（3）（本小题满分7分）

    选修4-5：不等式选讲 解不等式∣2x-1∣<∣x∣+1

     

     

     

     

     

     

    查看答案和解析>>

    （本题满分14分）

    已知函数f（x）=lnx+

    （Ⅰ）求函数f（x）的单调区间；

    （Ⅱ）设m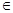R，对任意的a∈（-l，1），总存在xo∈[1，e]，使得不等式ma － (xo)<0成立，求实数m的取值范围；

    （Ⅲ）证明：ln2 l+ 1n22,+…+ln2 n>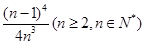∈N*）．

     

    查看答案和解析>>


    同步练习册答案