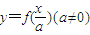[例1]求下列函数的反函数: (1),(2), (3); 解:(1)由得. ∴. ∴所求函数的反函数为; (2)当时..当时. 得. ∴所求函数的反函数为 (3)由得. ∴. ∴所求反函数为. 提炼方法:1.求反函数的步骤:2.分段函数的反函数要分段求. 并注意原函数在每段上的值域. [例2]已知函数f(x)=的图象关于直线y=x对称.求实数m. 解:∵f(x)的图象关于直线y=x对称.又点(5.0)在f(x)的图象上.∴点(0.5)也在f(x)的图象上.即-=5.得m=-1. 法二:由.有反函数.由于f(x)的图象关于y=x对称.与f -1(x)相同.比较系数得m=-1. 提炼方法:法1.找一特殊点(5,0)的对称点在图象上; 法2.f(x) 与f -1(x)相同,比较系数. [例3]已知函数f(x)=2(-)(a>0.且a≠1). (1)求反函数y=f-1(x), (2)判定f-1(x)的奇偶性, (3)解不等式f-1(x)>1. 解:(1)化简.得f(x)=. 设y=.则ax=.∴x=loga. ∴所求反函数为 y=f-1(x)=loga(-1<x<1). (2)∵f-1(-x)=loga=loga()-1=-loga=-f-1(x). ∴f-1(x)是奇函数. (3)loga>1. 当a>1时. 原不等式>a<0. ∴<x<1. 当0<a<1时.原不等式 解得 ∴-1<x<. 综上.当a>1时.所求不等式的解集为(.1), 当0<a<1时.所求不等式的解集为(-1.). [研究.欣赏] 已知函数f(x)是函数y=-1(x∈R)的反函数.函数g(x)的图象与函数y=的图象关于直线y=x-1成轴对称图形.记F(x)=f(x)+g(x). (1)求F(x)的解析式及定义域. (2)试问在函数F(x)的图象上是否存在这样两个不同点A.B.使直线AB恰好与y轴垂直?若存在.求出A.B两点坐标,若不存在.说明理由. 解:(1)由y=-1(x∈R).得10x=.x=lg.∴f(x)=lg(-1<x<1). 设P(x.y)是g(x)图象上的任意一点.则P关于直线y=x-1的对称点P′的坐标为(1+y.x-1).由题设知点P′(1+y.x-1)在函数y=的图象上.∴x-1=. ∴y=.即g(x)=(x≠-2). ∴F(x)=f(x)+g(x)=lg+.其定义域为{x|-1<x<1}. (2)∵f(x)=lg=lg(-1+)(-1<x<1)是减函数.g(x)=(-1<x<1)也是减函数.∴F(x)在上是减函数. 故不存在这样两个不同点A.B.使直线AB恰好与y轴垂直. 点评:本题是一道综合题.解决第(2)小题常用的方法是反证法.但本题巧用单调性法使问题变得简单明了. 【
查看更多】
题目列表(包括答案和解析)
例2.设f(x)是定义在[-3,
]上的函数,求下列函数的定义域(1)
y=f(-2)(2)
y=f()(a≠0)
查看答案和解析>>
例1.求下列函数的定义域
(1)
y=
,
(2)y=log
a[log
a(log
ax)]
,
(3)
y=+lgsinx
.
查看答案和解析>>
例1.求下列函数的值域
(1)
y=(2)
y=(3)y=sinx+cosx+sinxcosx
(4)
y=x+(2≤x≤5)(5)
y=.
查看答案和解析>>
例1.求下列函数的定义域
(1)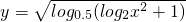 ______,
______,
(2)y=loga[loga(logax)]______,
(3)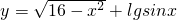 ______.
______.
查看答案和解析>>
例2.设f(x)是定义在[-3,
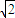
]上的函数,求下列函数的定义域(1)

(2)
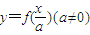
查看答案和解析>>

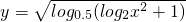 ______,
______,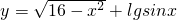 ______.
______. ]上的函数,求下列函数的定义域(1)
]上的函数,求下列函数的定义域(1) (2)
(2)