
题目列表(包括答案和解析)
 竖直平面内固定一内壁光滑半径为r的圆形细弯管,如图所示.管内有一质量为m,直径很小的小球(可视为质点)做圆周运动,小球在最高点时,恰与管壁无相互作用力,则小球通过最低点时管壁对小球的作用力大小为( )
竖直平面内固定一内壁光滑半径为r的圆形细弯管,如图所示.管内有一质量为m,直径很小的小球(可视为质点)做圆周运动,小球在最高点时,恰与管壁无相互作用力,则小球通过最低点时管壁对小球的作用力大小为( ) 竖直平面内有一个半径为R的光滑圆环轨道,一个质量为m的小球穿在圆环上做圆周运动,如图所示,到达最高点C时的速率vc=
竖直平面内有一个半径为R的光滑圆环轨道,一个质量为m的小球穿在圆环上做圆周运动,如图所示,到达最高点C时的速率vc=
|
竖直平面内固定一内壁光滑半径为r的圆形细弯管,如图所示。管内有一质量为m,直径很小的小球(可视为质点)做圆周运动,小球在最高点时,恰与管壁无相互作用力,则小球通过最低点时管壁对小球的作用力大小为
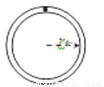
A.4mg B.5mg C.6mg D.7mg
竖直平面内固定一内壁光滑半径为r的圆形细弯管,如图所示。管内有一质量为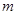 ,直径很小的小球(可视为质点)做圆周运动,小球在最高点时,恰与管壁无相互作用力,则小球通过最低点时管壁对小球的作用力大小为( )
,直径很小的小球(可视为质点)做圆周运动,小球在最高点时,恰与管壁无相互作用力,则小球通过最低点时管壁对小球的作用力大小为( )

A.4mg B.5mg C.6mg D.7mg
竖直平面内固定一内壁光滑半径为r的圆形细弯管,如图所示。管内有一质量为m,直径很小的小球(可视为质点)做圆周运动,小球在最高点时,恰与管壁无相互作用力,则小球通过最低点时管壁对小球的作用力大小为 
| A.4mg | B.5mg | C.6mg | D.7mg |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com