
题目列表(包括答案和解析)
抛物线![]() 的准线方程是 ( )
的准线方程是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
抛物线![]() 的准线方程是 ( )
的准线方程是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
抛物线 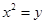 的准线方程是( )
的准线方程是( )
A.4 x + 1 = 0 B.4 y + 1 =" 0"
C.2 x + 1 = 0 D.2 y + 1 =" 0"
抛物线 的准线方程是( )
的准线方程是( )
A. B.
B. C.
C. D.
D.
抛物线 的准线方程是( )。
的准线方程是( )。
 .
.
 .
.
 .
.
 .
.
一、选择题:
BDDCB BBAAC AC
二、填空题:
13. 14.6 15.
14.6 15. 16.
16.
|