
题目列表(包括答案和解析)
.若函数![]() ,
,![]() 的表达式是( )
的表达式是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
.若 ,则
,则
A. | B. | C. | D. |
.若向量 满足
满足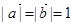 ,
, 与
与 的夹角为600,则
的夹角为600,则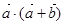 的值为( )
的值为( )
A. | B. | C.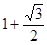 | D.2 |
.若过点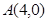 的直线
的直线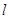 与曲线
与曲线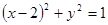 有公共点,则直线
有公共点,则直线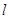 的斜率最小值为
( )
的斜率最小值为
( )
A.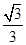 B.
B.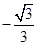 C.
C.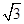 D.
D. 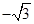
.若函数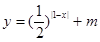 的图象与
的图象与 轴有公共点,则
轴有公共点,则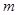 的取值范围是( )
的取值范围是( )
A. B.
B.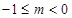 C.
C.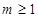 D.
D.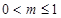
一、选择题:
DDABD ACCBB CD
二、填空题:
13. 14.
14. 15.32 16.
15.32 16. 
三、解答题:
17.解:(I) 服从超几何分布
服从超几何分布

 3分
3分
(II) 5分
5分
 7分
7分
 9分
9分
Y
5
6
7
P



…………10分
|