
题目列表(包括答案和解析)
设集合A={x|-1≤x≤2}, B={x|x2-(2m+1) x+2m<0}.
(1)当m<![]() 时,化简集合B;
时,化简集合B;
(2)若A∪B=A,求实数m的取值范围;
(3)若(CUA) ∩B中只有一个整数,求实数m的取值范围.
设集合A={x|-1≤x≤2},B={x|x2-(2m+1)x+2m<0}.
(1)当m<![]() 时,化简集合B;
时,化简集合B;
(2)若A∪B=A,求实数m的取值范围;
(3)若![]() ∩B中只有一个整数,求实数m的取值范围.
∩B中只有一个整数,求实数m的取值范围.
设集合A={x|-1≤x≤2}, B={x|x2-(2m+1) x+2m<0}.
(1)当m<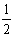 时,化简集合B;
时,化简集合B;
(2)若A∪B=A,求实数m的取值范围;
(3)若(CUA) ∩B中只有一个整数,求实数m的取值范围.
我们常用构造等式对同一个量算两次的方法来证明组合恒等式,如由等式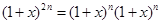 可得,左边
可得,左边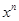 的系数为
的系数为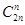 ,
,
而右边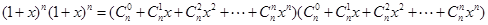 ,
, 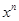 的系数为
的系数为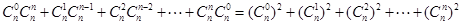 ,
,
由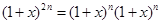 恒成立,可得
恒成立,可得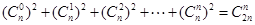 .
.
利用上述方法,化简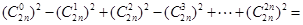 .
.
(a
| ||||||||
|
| ||
| 6 |
| 11 |
| 6 |
| 25 |
| 6 |
| ||
| 6 |
| 11 |
| 6 |
| 25 |
| 6 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com