
题目列表(包括答案和解析)
定义域为D的函数 同时满足条件:①常数
同时满足条件:①常数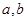 满足
满足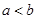 ,区间
,区间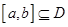 ,②使
,②使 在
在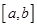 上的值域为
上的值域为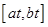 ,那么我们把
,那么我们把 叫做
叫做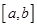 上的“
上的“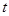 级矩形”函数.函数
级矩形”函数.函数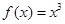 是
是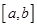 上的“1级矩形”函数,则满足条件的常数对
上的“1级矩形”函数,则满足条件的常数对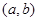 共有( )
共有( )
A.1对 B.2对 C.3对 D.4对
定义域为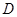 的函数
的函数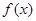 同时满足条件:①常数
同时满足条件:①常数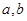 满足
满足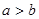 ,区间
,区间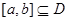 ,②使
,②使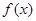 在
在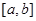 上的值域为
上的值域为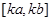
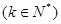 ,那么我们把
,那么我们把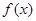 叫做
叫做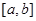 上的“
上的“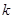 级矩形”函数.函数
级矩形”函数.函数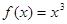 是
是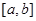 上的“1级矩形”函数,则满足条件的常数对
上的“1级矩形”函数,则满足条件的常数对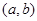 共有( )
共有( )
 1对
1对  2对
2对
 3对
3对  4对
4对
| 1-x |
| ax |
| 1-x |
| ax |
| a+b |
| b |
| 1 |
| a+b |
 是[1,+∞)上的增函数.
是[1,+∞)上的增函数. 的定义域为[1,+∞),根据所给函数g(x)的下确界的定义,求出当a=1时函数f(x)的下确界.
的定义域为[1,+∞),根据所给函数g(x)的下确界的定义,求出当a=1时函数f(x)的下确界.
函数的概念
设A,B是非空的数集,如果按某个确定的对应关系f,使对于集合A中的任意一个x,在集合B中都有________的数f(x)和它对应,那么就称f:A→B为从集合A到集合B的函数,记作y=f(x),x∈A.
其中x叫________,x的取值范围A叫做函数y=f(x)的________;与x的值相对应的y的值叫做函数值,函数值的集合{f(x)|x∈A}(![]() B)叫做函数y=f(x)的________.函数符号y=f(x)表示“y是x的函数”,有时简记作函数________.
B)叫做函数y=f(x)的________.函数符号y=f(x)表示“y是x的函数”,有时简记作函数________.
(1)函数实际上就是集合A到集合B的一个特殊对应f:A→B,这里A、B为________的数集.
(2)A:定义域;{f(x)|x∈A}:值域,其中{f(x)|x∈A}________B;f:对应法则,x∈A,y∈B.
(3)函数符号:y=f(x)y是x的函数,简记f(x).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com