
题目列表(包括答案和解析)
A.大于m B.小于m
C.等于m D.与m的大小关系无法确定
(2007
北京海淀模拟)函数y=kx+b,其中k,b(k≠0)是常数,其图象是一条直线,称这个函数为线性函数,对于非线性可导函数f(x),在点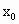 附近一点x的函数值f(x),可以用如下方法求其近似代替值:
附近一点x的函数值f(x),可以用如下方法求其近似代替值: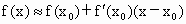 .利用这一方法,
.利用这一方法,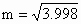 的近似代替值
的近似代替值
[
]|
A .大于m |
B .小于m |
|
C .等于m |
D .与m的大小关系无关 |
函数y=kx+b,其中k,b(k≠0)是常数,其图像是一条直线,称这个函数为线性函数.对于非线性可导函数f(x),在点x0附近一点x的函数值f(x),可以用如下方法求其近似代替值:f(x)≈f(x0)+![]() (x0)(x-x0).利用这一方法,m=
(x0)(x-x0).利用这一方法,m=![]() 的近似代替值
的近似代替值
A.大于m
B.小于m
C.等于m
D.与m的大小关系无法确定
要研究可导函数f(
x)=(1+x)n(n∈N*)在某点x0处的瞬时变化率,有两种方案可供选择:①直接求导,得到![]() =
=
设可导函数f(x)满足条件![]() =-1,求曲线y=f(x)在点(2,f(2))处的切线的斜率.
=-1,求曲线y=f(x)在点(2,f(2))处的切线的斜率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com