
题目列表(包括答案和解析)
| 4x+2 |
| x+3 |
| ax+b |
| cx+d |
| an-x1 |
| an-x2 |
| lim |
| n→∞ |
已知函数 的图象过坐标原点O,且在点
的图象过坐标原点O,且在点 处的切线的斜率是
处的切线的斜率是 .
.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)求 在区间
在区间 上的最大值;
上的最大值;
(Ⅲ)对任意给定的正实数 ,曲线
,曲线 上是否存在两点P、Q,使得
上是否存在两点P、Q,使得 是以O为直角顶点的直角三角形,且此三角形斜边中点在
是以O为直角顶点的直角三角形,且此三角形斜边中点在 轴上?说明理由.
轴上?说明理由.
【解析】第一问当 时,
时, ,则
,则 。
。
依题意得: ,即
,即 解得
解得
第二问当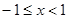 时,
时, ,令
,令 得
得 ,结合导数和函数之间的关系得到单调性的判定,得到极值和最值
,结合导数和函数之间的关系得到单调性的判定,得到极值和最值
第三问假设曲线 上存在两点P、Q满足题设要求,则点P、Q只能在
上存在两点P、Q满足题设要求,则点P、Q只能在 轴两侧。
轴两侧。
不妨设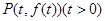 ,则
,则 ,显然
,显然
∵ 是以O为直角顶点的直角三角形,∴
是以O为直角顶点的直角三角形,∴
即 (*)若方程(*)有解,存在满足题设要求的两点P、Q;
(*)若方程(*)有解,存在满足题设要求的两点P、Q;
若方程(*)无解,不存在满足题设要求的两点P、Q.
(Ⅰ)当 时,
时, ,则
,则 。
。
依题意得: ,即
,即 解得
解得
(Ⅱ)由(Ⅰ)知,
①当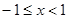 时,
时, ,令
,令 得
得
当 变化时,
变化时,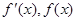 的变化情况如下表:
的变化情况如下表:
|
|
|
0 |
|
|
|
|
|
— |
0 |
+ |
0 |
— |
|
|
|
极小值 |
单调递增 |
极大值 |
|
又 ,
, ,
, 。∴
。∴ 在
在 上的最大值为2.
上的最大值为2.
②当 时,
时,  .当
.当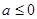 时,
时,  ,
, 最大值为0;
最大值为0;
当 时,
时,  在
在 上单调递增。∴
上单调递增。∴ 在
在 最大值为
最大值为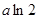 。
。
综上,当 时,即
时,即 时,
时, 在区间
在区间 上的最大值为2;
上的最大值为2;
当 时,即
时,即 时,
时, 在区间
在区间 上的最大值为
上的最大值为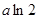 。
。
(Ⅲ)假设曲线 上存在两点P、Q满足题设要求,则点P、Q只能在
上存在两点P、Q满足题设要求,则点P、Q只能在 轴两侧。
轴两侧。
不妨设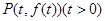 ,则
,则 ,显然
,显然
∵ 是以O为直角顶点的直角三角形,∴
是以O为直角顶点的直角三角形,∴
即 (*)若方程(*)有解,存在满足题设要求的两点P、Q;
(*)若方程(*)有解,存在满足题设要求的两点P、Q;
若方程(*)无解,不存在满足题设要求的两点P、Q.
若 ,则
,则 代入(*)式得:
代入(*)式得:
即 ,而此方程无解,因此
,而此方程无解,因此 。此时
。此时 ,
,
代入(*)式得:  即
即 (**)
(**)
令
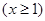 ,则
,则
∴ 在
在 上单调递增, ∵
上单调递增, ∵  ∴
∴ ,∴
,∴ 的取值范围是
的取值范围是 。
。
∴对于 ,方程(**)总有解,即方程(*)总有解。
,方程(**)总有解,即方程(*)总有解。
因此,对任意给定的正实数 ,曲线
,曲线 上存在两点P、Q,使得
上存在两点P、Q,使得 是以O为直角顶点的直角三角形,且此三角形斜边中点在
是以O为直角顶点的直角三角形,且此三角形斜边中点在 轴上
轴上
2.A解析:由![]() 知函数在
知函数在![]() 上有零点,又因为函数在(0,+
上有零点,又因为函数在(0,+![]() )上是减函数,所以函数y=f(x) 在(0,+
)上是减函数,所以函数y=f(x) 在(0,+![]() )上有且只有一个零点不妨设为
)上有且只有一个零点不妨设为![]() ,则
,则![]() ,又因为函数是偶函数,所以
,又因为函数是偶函数,所以![]() =0并且函数在(0,+
=0并且函数在(0,+![]() )上是减函数,因此-
)上是减函数,因此-![]() 是(-
是(-![]() ,0)上的唯一零点,所以函数共有两个零点
,0)上的唯一零点,所以函数共有两个零点
下列叙述中,是随机变量的有( )
①某工厂加工的零件,实际尺寸与规定尺寸之差;②标准状态下,水沸腾的温度;③某大桥一天经过的车辆数;④向平面上投掷一点,此点坐标.
A.②③ B.①② C.①③④ D.①③
设A是由m×n个实数组成的m行n列的数表,满足:每个数的绝对值不大于1,且所有数的和为零,记s(m,n)为所有这样的数表构成的集合。
对于A∈S(m,n),记ri(A)为A的第ⅰ行各数之和(1≤ⅰ≤m),Cj(A)为A的第j列各数之和(1≤j≤n):
记K(A)为∣r1(A)∣,∣R2(A)∣,…,∣Rm(A)∣,∣C1(A)∣,∣C2(A)∣,…,∣Cn(A)∣中的最小值。
(1) 对如下数表A,求K(A)的值;
|
1 |
1 |
-0.8 |
|
0.1 |
-0.3 |
-1 |
(2)设数表A∈S(2,3)形如
|
1 |
1 |
c |
|
a |
b |
-1 |
求K(A)的最大值;
(3)给定正整数t,对于所有的A∈S(2,2t+1),求K(A)的最大值。
【解析】(1)因为 ,
,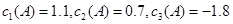
所以
(2) 不妨设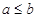 .由题意得
.由题意得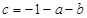 .又因为
.又因为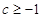 ,所以
,所以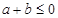 ,
,
于是 ,
,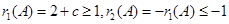 ,
,
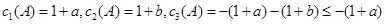
所以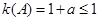 ,当
,当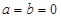 ,且
,且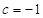 时,
时,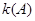 取得最大值1。
取得最大值1。
(3)对于给定的正整数t,任给数表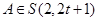 如下,
如下,
|
|
|
… |
|
|
|
|
… |
|
任意改变A的行次序或列次序,或把A中的每一个数换成它的相反数,所得数表
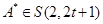 ,并且
,并且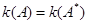 ,因此,不妨设
,因此,不妨设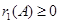 ,
,
且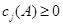
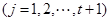 。
。
由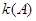 得定义知,
得定义知,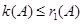 ,
,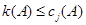
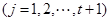
又因为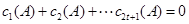
所以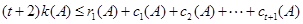
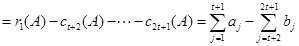
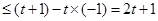
所以,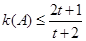
对数表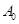 :
:
|
1 |
1 |
… |
1 |
|
… |
|
|
|
|
… |
|
-1 |
… |
-1 |
则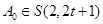 且
且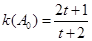 ,
,
综上,对于所有的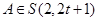 ,
,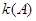 的最大值为
的最大值为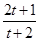
| 4x+2 |
| x+3 |
| ax+b |
| cx+d |
| an-x1 |
| an-x2 |
| lim |
| n→∞ |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com