
题目列表(包括答案和解析)
假设关于某设备的使用年限x和所支出的维修费y(万元)有如下的统计资料:

若由资料可知y和x呈相关关系,由表中数据算出线性回归方程![]() =bx+a中的b=1.23,据此估计,使用年限为10年时的维修费用是________万元.
=bx+a中的b=1.23,据此估计,使用年限为10年时的维修费用是________万元.
(参考公式:b= =
= ,a=
,a=![]() -b
-b![]() )
)
假设关于某设备的使用年限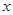 和所支出的维修费
和所支出的维修费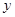 (万元),有如下的统计资料
(万元),有如下的统计资料
|
使用年限 |
2 |
3 |
4 |
5 |
6 |
|
维修费用 |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
若由资料可知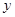 和
和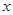 呈相关关系,由表中数据算出线性回归方程
呈相关关系,由表中数据算出线性回归方程 中的
中的 =
= ,据此估计,使用年限为10年时的维修费用是 万元.
,据此估计,使用年限为10年时的维修费用是 万元.
(参考公式: ,
, )
)
假设关于某设备的使用年限 和所支出的维修费
和所支出的维修费 (万元),有如下的统计资料:
(万元),有如下的统计资料:
|
使用年限 |
|
|
|
|
|
|
维修费用 |
|
|
|
|
|
若由资料可知 和
和 呈相关关系,由表中数据算出线性回归方程
呈相关关系,由表中数据算出线性回归方程 中的
中的 =
=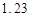 ,据此估计,使用年限为
,据此估计,使用年限为 年时的维修费用是
万元.
年时的维修费用是
万元.
假设关于某设备的使用年限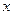 和所支出的维修费
和所支出的维修费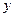 (万元),有如下的统计资料:
(万元),有如下的统计资料:
使用年限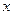 | 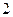 |  | 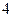 | 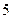 | 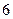 |
维修费用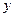 | 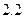 |  | 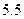 | 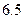 | 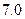 |
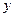 和
和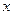 呈相关关系,由表中数据算出线性回归方程
呈相关关系,由表中数据算出线性回归方程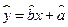 中的
中的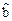 =
=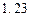 ,据此估计,使用年限为
,据此估计,使用年限为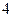 年时的维修费用是 万元.
年时的维修费用是 万元. 和所支出的维修费
和所支出的维修费 (万元),有如下的统计资料:
(万元),有如下的统计资料:使用年限 |  |  |  |  |  |
维修费用 |  |  |  |  |  |
 和
和 呈相关关系,由表中数据算出线性回归方程
呈相关关系,由表中数据算出线性回归方程 中的
中的 =
= ,据此估计,使用年限为
,据此估计,使用年限为 年时的维修费用是 万元.
年时的维修费用是 万元.
说明:
一、本解答指出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制定相应的评分细则.
二、对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应给分数的一半;如果后继部分的解答有较严重的错误,就不再给分.
三、解答右端所注分数,表示考生正确做到这一步应得的累加分数.
四、只给整数分数,选择题和填空题不给中间分.
一、选择题:本题考查基本知识和基本运算,每小题5分,满分50分.
1. A 2. C 3. C 4.C 5.D 6.D 7. B 8. D 9. B 10. C
二、填空题:本题考查基本知识和基本运算,每小题4分,满分20分.
11. 12.38 12. 5 13. 3 14.
14.  15.
②③
15.
②③
三、解答题:本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤.
16. 本小题主要考查正弦定理、三角函数的倍角公式、两角和公式等基本知识,考
查学生的运算求解能力. 满分13分.
解:(Ⅰ)由 ,知
,知 ………………………(2分)
………………………(2分)
又 ,得
,得 ,
,
 ,
, ………………………(5分)
………………………(5分)
故 ………………………(6分)
………………………(6分)
(Ⅱ) 由(Ⅰ)知 ,
,


 ………………………………(9分)
………………………………(9分)
 ,
,
当 ,即
,即 时,
时, 取得最大值为
取得最大值为 . ……………(13分)
. ……………(13分)
 17. 本题主要考查线线、线面、面面位置关系,线面角等基本知识,考查空间想像能力,运算求解能力和推理论证能力.
满分13分.
17. 本题主要考查线线、线面、面面位置关系,线面角等基本知识,考查空间想像能力,运算求解能力和推理论证能力.
满分13分.
 解:(Ⅰ)证明:如图,取
解:(Ⅰ)证明:如图,取 中点
中点 ,连结
,连结 ,
, ;
;

 ∥
∥ ,
, ∥
∥ ,
,
又 ,
, ,
,

 ,…………(3分)
,…………(3分)
四边形 为平行四边形,
为平行四边形,
 ∥
∥ ,
,
又 平面
平面 ,
, 平面
平面 ,
,
 ∥平面
∥平面 .
………………………(6分)
.
………………………(6分)
(Ⅱ)依题意知平面 平面
平面 ,
, ,
,
 平面
平面 ,得
,得
又 ,
, .
.
如图,以 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系 -xyz,
-xyz,
 ,可得
,可得 、
、 、
、 ,
,
 .
.
设平面 的一个法向量为
的一个法向量为 ,
,
由 得
得
解得 ,
, .
………………………(9分)
.
………………………(9分)
设线段 上存在一点
上存在一点 ,其中
,其中 ,则
,则 ,
,
 ,
,
依题意: ,即
,即 ,
,
可得 ,解得
,解得 (舍去).
(舍去).
所以 上存在一点
上存在一点 . …………(13分)
. …………(13分)
18.本题主要考查函数与导数等基本知识,考查运用数学知识分析问题与解决问题的能力,
考查应用意识. 满分13分.
解:(Ⅰ)依题意,
销售价提高后为6000(1+ )元/台,月销售量为
)元/台,月销售量为 台……………(2分)
台……………(2分)
则 ……………………(4分)
……………………(4分)
即 . ……………………(6分)
. ……………………(6分)
(Ⅱ)
令 ,得
,得 ,
,
解得 舍去).
……………………(9分)
舍去).
……………………(9分)
当 当
当
当 时,
时, 取得最大值.
取得最大值.
此时销售价为 元.
元.
答:笔记本电脑的销售价为9000元时,电脑企业的月利润最大.…………………(13分)
 19.本题主要考查直线与椭圆的位置关系、不等式的解法等基本知识,考查运算求解能力和分析问题、解决问题的能力.
满分13分
19.本题主要考查直线与椭圆的位置关系、不等式的解法等基本知识,考查运算求解能力和分析问题、解决问题的能力.
满分13分
解:(Ⅰ)因为椭圆 的一个焦点是(1,0),所以半焦距
的一个焦点是(1,0),所以半焦距 =1.
=1.
因为椭圆两个焦点与短轴的一个端点构成等边三角形.
所以 ,解得
,解得
所以椭圆的标准方程为 . …(4分)
. …(4分)
 (Ⅱ)(i)设直线
(Ⅱ)(i)设直线 :
: 与
与 联立并消去
联立并消去 得:
得: .
.
记 ,
, ,
,
 ,
,
 . ……………(5分)
. ……………(5分)
由A关于 轴的对称点为
轴的对称点为 ,得
,得 ,
,
根据题设条件设定点为 (
( ,0),
,0),
得 ,即
,即 .
.
所以

即定点 (1 , 0).
……………………………………(8分)
(1 , 0).
……………………………………(8分)
(ii)由(i)中判别式 ,解得
,解得 .
.
可知直线 过定点
过定点 (1,0).
(1,0).
所以 ……………(10分)
……………(10分)
得 , 令
, 令
记 ,得
,得 ,当
,当 时,
时, .
.
 在
在 上为增函数.
上为增函数.
所以
 ,
,
得 .
.
故△OA1B的面积取值范围是 .
……………(13分)
.
……………(13分)
20. 本题主要考查函数的单调性、等差数列、不等式等基本知识,考查运用合理的推理证明解
决问题的方法,考查分类与整合及化归与转化等数学思想. 满分14分.
解:(Ⅰ)因为 ,
,
所以 .
………………(1分)
.
………………(1分)
(i)当 时,
时, .
.
(ii)当 时,由
时,由 ,得到
,得到 ,知在
,知在 上
上 .
.
(iii)当 时,由
时,由 ,得到
,得到 ,知在
,知在 上
上 .
.
综上,当 时,
时, 递增区间为
递增区间为 ;当
;当 时,
时,  递增区间为
递增区间为 .
………………………………………(4分)
.
………………………………………(4分)
(Ⅱ)(i)因为 ,
,
所以 ,即
,即 ,
,
 ,即
,即 . ……………………………………(6分)
. ……………………………………(6分)
因为 ,
,
当 时,
时, ,
,
当 时,
时, ,
,
所以 .
…………………………(8分)
.
…………………………(8分)
又因为 ,
,
所以令 ,则
,则
得到 与
与 矛盾,所以
矛盾,所以 不在数列
不在数列 中. ………(9分)
中. ………(9分)
(ii)充分性:若存在整数 ,使
,使 .
.
设 为数列
为数列 中不同的两项,则
中不同的两项,则
 .
.
又 且
且 ,所以
,所以 .
.
即 是数列
是数列 的第
的第 项. ……………………(10分)
项. ……………………(10分)
必要性:若数列 中任意不同两项之和仍为数列
中任意不同两项之和仍为数列 中的项,
中的项,
则 ,
, ,(
,( ,
, 为互不相同的正整数)
为互不相同的正整数)
则 ,令
,令 ,
,
得到
 ,
,
所以 ,令整数
,令整数 ,所以
,所以 . ……(11 分)
. ……(11 分)
下证整数
若设整数 则
则 .令
.令 ,
,
由题设取 使
使
即 ,所以
,所以
即 与
与 相矛盾,所以
相矛盾,所以 .
.
综上, 数列 中任意不同两项之和仍为数列
中任意不同两项之和仍为数列 中的项的充要条件是存在整数
中的项的充要条件是存在整数 ,使
,使 .
……………………(14分)
.
……………………(14分)
21. (1)本题主要考查矩阵乘法、逆矩阵与变换等基本知识,考查运算求解能力, 满分7分.
解: ,即
,即 ,
,
所以 得
得 ……………………(4分)
……………………(4分)
即M=
 ,由
,由 得
得
 .
.
或
 =1
=1 ,
, 
 . …………………(7分)
. …………………(7分)
(2)本题主要考查圆极坐标方程和直线参数方程等基本知识,考查运算求解能力,考查化归与转化思想. 满分7分.
解:曲线 的极坐标方程
的极坐标方程 可化为
可化为 ,
,
其直角坐标方程为 ,即
,即 . ……………(2分)
. ……………(2分)
直线 的方程为
的方程为 .
.
所以,圆心到直线 的距离
的距离 ……………………(5分)
……………………(5分)
所以, 的最小值为
的最小值为 .
…………………………(7分)
.
…………………………(7分)
(3)本题主要考查柯西不等式与不等式解法等基本知识,考查化归与转化思想. 满分7分.
解:由柯西不等式:
 . …………(3分)
. …………(3分)
因为
所以 ,即
,即 .
.
因为 的最大值是7,所以
的最大值是7,所以 ,得
,得 ,
,
当 时,
时, 取最大值,
取最大值,
所以 .
………………………………………(7分)
.
………………………………………(7分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com