
题目列表(包括答案和解析)
设椭圆![]() 的左焦点为
的左焦点为![]() ,左准线
,左准线![]() 与
与![]() 轴交于点
轴交于点![]() ,过
,过![]() 点作直线
点作直线![]() 交椭圆于A、B两点.
交椭圆于A、B两点.
(1)求椭圆的方程;
(2)若以![]() 为直径的圆过点
为直径的圆过点![]() ,试求直线
,试求直线![]() 的方程.
的方程.
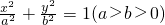 的左焦点为F1(-2,0),左准线l1与x轴交于点N(-3,0),过N点作直线l交椭圆于A、B两点.
的左焦点为F1(-2,0),左准线l1与x轴交于点N(-3,0),过N点作直线l交椭圆于A、B两点. 的左焦点为F1(-2,0),左准线与x轴交于点N(-3,0),过点N倾斜角为30°的直线m交椭圆于A,B两点,
的左焦点为F1(-2,0),左准线与x轴交于点N(-3,0),过点N倾斜角为30°的直线m交椭圆于A,B两点, 的左焦点为F1(-2,0),左准线l1与x轴交于点N(-3,0),过N点作直线l交椭圆于A、B两点.
的左焦点为F1(-2,0),左准线l1与x轴交于点N(-3,0),过N点作直线l交椭圆于A、B两点. 的左焦点为F,上顶点为A,直线AF的倾斜角为45°,
的左焦点为F,上顶点为A,直线AF的倾斜角为45°,
一、选择题:
1.解析:B.由 且
且 能够推出
能够推出 ;反之,由
;反之,由 只能推出
只能推出 或
或 ,而不能推出
,而不能推出 且
且 .故“
.故“ ”是“
”是“ 且
且 ”的必要不充分条件,故选B.
”的必要不充分条件,故选B.
评析:有关充要条件的判定问题,概念性较强,进行判断时,必须紧扣概念.一方面,要正确理解充要条件本身的概念,进行双向推理,准确判断;另一方面,还要注意根据具体问题所涉及到的数学概念来思考.本题中,弄清并集和交集概念中“或”与“且”的关系显得很重要.
2.解析:B.∵△= .要使函数
.要使函数 的一个零点在
的一个零点在 内,必须满足条件:
内,必须满足条件: ,即
,即 ,
,
∴ ,∴实数k的取值范围为(2,3).
,∴实数k的取值范围为(2,3).
3.解析:D.化简复数 可得
可得 ,∴
,∴ ,
,
故选D.
4.解析:B 先作出直线A1B与平面BC1D1所成角,再通过解三角形求出其正切值.如图,连结 交
交 于
于 ,连结
,连结 .由
.由 ,
, ,又
,又 ,得
,得 ,所以
,所以 就是直线A1B与平面BC1D1所成角.在直角
就是直线A1B与平面BC1D1所成角.在直角 中,求得
中,求得 ,故选B.
,故选B.
评析:平面的斜线与平面所成的角,就是这条斜线与它在该平面上
 的射影所成的锐角,根据题目的条件作出斜线在该平面上的射影
的射影所成的锐角,根据题目的条件作出斜线在该平面上的射影
是实现解题的关键,而作射影的关键则是作出平面的垂线,要注
意面面垂直的性质在作平面的垂线时的应用.
5.解析:
A.特值法.取B=0,A=1,C=-1,则M(1, ),
),
N(1,- ), ∴
), ∴ = x1x2+y1y2 =-2.故选A .
= x1x2+y1y2 =-2.故选A .
6.解析
B.设点 是函数
是函数 上的任意一点,点
上的任意一点,点 关于点
关于点 的对称点为
的对称点为 ,则
,则 由
由 在
在 上,
上,
得 ,∴
,∴ ,即
,即 .故选B.
.故选B.
7.解析: C.图象法.由 的图象可得,
的图象可得, 在
在 上是增函数,在
上是增函数,在 上是减函数,又
上是减函数,又 是偶函数,∴
是偶函数,∴ ,
,
∴ ,解得
,解得 .故选C.
.故选C.
8.解析:B,由 ,得:
,得: ,即
,即 ,
,
解之得 ,由于
,由于 ,故
,故 ;选B
;选B
9.解析: B.如果四块均不同色,则有 种涂法;如果有且仅有两块同色,它们必是相对的两块,有
种涂法;如果有且仅有两块同色,它们必是相对的两块,有 种涂法;如果两组相对的两块分别同色,则有
种涂法;如果两组相对的两块分别同色,则有 种涂法.根据分类计数原理,得到涂色方法种数为
种涂法.根据分类计数原理,得到涂色方法种数为 (种),故选B.
(种),故选B.
10.解析:选D.①②③易于判断其真。 .
.
 ,即曲线上任一点P(x,y)在单位图
,即曲线上任一点P(x,y)在单位图 外,(点(±1,0)在圆上),
外,(点(±1,0)在圆上),
则S>π?12=π
评析:f(x,y)=f(x,-y) 曲线f(x,y)=0,关于x轴对称;
曲线f(x,y)=0,关于x轴对称;
f(x,y)=f(-x, y) 曲线f(x,y)=0,关于y轴对称;
曲线f(x,y)=0,关于y轴对称;
f(x,y)=f(-x, -y) 曲线f(x,y)=0,关于原点对称。
曲线f(x,y)=0,关于原点对称。
 11.解析:D,在EF上任意取一点M,直线
11.解析:D,在EF上任意取一点M,直线 与M确定一个平面,
与M确定一个平面,
这个平面与CD有且仅有1个交点N, 当M取不同的位置就确
定不同的平面,从而与CD有不同的交点N,而直线MN与这
3条异面直线都有交点的.如右图:
评析:本题主要考查立体几何中空间直线相交问题,考查学生
的空间想象能力。
12.解析:C.P(X=8)= ,P(X=7)=
,P(X=7)= ,
,
P(X=6)= , 所以P(X≥6)=
, 所以P(X≥6)= ,
,
即线路信息畅通的概率为 ,故选C.
,故选C.
二、填空题:
13.解析: .由
.由 ,得
,得 ,即
,即 ,又由
,又由 ,得
,得 ,∴
,∴ ,
,
于是,

 .
.
14. 解析: .如图,
.如图, 过点
过点 ,
, .
.
 在点
在点 处取得最小值,
处取得最小值, 点在直线
点在直线
 上,
上, ,∴
,∴ .
.
评析:简单的线性规划问题,其约束条件是平面上的一个
多边形闭区域,或者是向某一方向无限延展的半闭区域,而目标函数一般在边界的顶点处取得最值.解题时通常运用图解法,根据题意画出图形,从图形中寻求思路、获得答案,体现了数形结合的思想方法.
15.解析:f(x)=x2+2x+1 .设f(x)=ax2+bx+c
(a≠0),则△=b2-
∴ ,故 f(x)=x2+2x+1 .
,故 f(x)=x2+2x+1 .
16.解析:椭圆 与双曲线
与双曲线 的焦距相等.由椭圆
的焦距相等.由椭圆 与双曲线
与双曲线 的焦距相等,分析椭圆和双曲线的标准方程中参数之间的关系,运用类比推理的方法,不难得到推广后的一个命题为:椭圆
的焦距相等,分析椭圆和双曲线的标准方程中参数之间的关系,运用类比推理的方法,不难得到推广后的一个命题为:椭圆 与双曲线
与双曲线 的焦距相等.
的焦距相等.
评析:推广命题有多种方法,其中类比推理是一种常用方法.值得指出的是,本题的答案不唯一,例如,我们还可以得到推广后的更具一般性的命题:椭圆 与双曲线
与双曲线
 的焦距相等.
的焦距相等.
三、解答题:
17.解析:(Ⅰ) ,在
,在 中,由余弦定理,
中,由余弦定理,
得 ,
,
∴ ,
,
 (2分)
(2分)
由 ,
, ,
,
由 得,
得, ,
,
∴ ,从而
,从而
 (4分)
(4分)
由题意可知 ,∴
,∴ ,
,
 (5分)
(5分)
又∵△BCD是 ,∴
,∴ 当
当 时,则
时,则 ,由
,由 ,
,
∴ ;
;
 当
当 时,则
时,则 ,由
,由 ,∴
,∴ ;
;
综上, .
.
 (7分)
(7分)
(Ⅱ)由(1)知 ,∴向量
,∴向量 与
与 的夹角为
的夹角为 ,
,  (9分)
(9分)
 当
当 时,
时, ,
, ,
,
∴ .
.
 (10分)
(10分)
 当
当 时,
时, ,
, ,
,
∴ .
.
 (12分)
(12分)
评析:本题考查平面向量和解三角形的基础知识,考查分类讨论的思想方法.求解时容易发生的错误是:(1)将条件“△BCD是直角三形”当作“△BCD是以角 是直角三形”来解,忽略对
是直角三形”来解,忽略对 为直角的情况的讨论;(2)在计算
为直角的情况的讨论;(2)在计算 时,将
时,将 当作向量
当作向量 与
与 的夹角,忽略了确定两个向量的夹角时必须将它们的起点移到一起.暴露出思维的不严谨和概念理解的缺陷,在复习中要引起重视,加强训练.
的夹角,忽略了确定两个向量的夹角时必须将它们的起点移到一起.暴露出思维的不严谨和概念理解的缺陷,在复习中要引起重视,加强训练.
18.解析: (Ⅰ)做了三次实验,至少两次实验成功的情形有两种:
(1)恰有两次成功,其概率为 ;
;
 (2分)
(2分)
(2)三次都成功,其概率为 .
.
 (4分)
(4分)
故得所求之概率为 .
.  (6分)
(6分)
(Ⅱ)在第4次成功之前,共做了6次试验,其中三次成功、三次失败,且恰有两次连续失败,其各种可能情况的种数为 .
.
 (10分)
(10分)
因此,所求之概率为 .
.
 (12分)
(12分)
19.解析:(Ⅰ)∵SB=SC,AB=AC,M为BC中点,
∴SM⊥BC,AM⊥BC.  (2分)
(2分)
由棱锥的侧面积等于底面积的2倍,即

得 .
.
 (4分)
(4分)
(Ⅱ)作正三棱锥的高SG,则G为正三角形ABC的中心,G在AM上,
∵SM⊥BC,AM⊥BC,
∴∠SMA是二面角S―BC―A的平面角. (6分)
(6分)
在Rt△SGM中,∵ ∴∠SMA=∠SMG=60°,
∴∠SMA=∠SMG=60°,
即二面角S―BC―A的大小为60°.  (8分)
(8分)
(Ⅲ)∵△ABC的边长是3,
∴ ,
,  (10分)
(10分)
∴ .
.  (12分)
(12分)
评析计算二面角大小,既可以根据二面角的定义,通过作出二面角的平面角,再解三角形求角,也可以运用向量方法,转化为计算两个平面的法向量的夹角.做题时要考虑前后联系,注意选择简便的方法.
20.解析:(Ⅰ)证明:假设存在一个实数,使{an}是等比数列,则有 ,即
,即
( )2=
)2= 2
2 矛盾.
矛盾.
所以{an}不是等比数列.
 (3分)
(3分)
(Ⅱ)证明:∵


 又
又 由上式知
由上式知
 故当
故当 数列{bn}是以
数列{bn}是以 为首项,
为首项, 为公比的等比数列.
为公比的等比数列.
 (7分)
(7分)
(Ⅲ)当 由(Ⅱ)得
由(Ⅱ)得 于是
于是
 当
当 时,
时, ,从而
,从而 上式仍成立.
上式仍成立.
要使对任意正整数n , 都有
即
 (9分)
(9分)
令
当n为正奇数时, 当n为正偶数时,
当n为正偶数时,
 于是可得
于是可得
综上所述,存在实数 ,使得对任意正整数
,使得对任意正整数 ,都有
,都有
 的取值范围为
的取值范围为
 (12分)
(12分)
评析:(1)求解等差数列与等比数列的有关问题,定义、公式和性质是主要工具,要注意抓住基本量───首项和公差(公比),方程思想、化归思想和运算能力是考查的重点;(2)正面求解,直接证明难以突破时,可以考虑从反面入手,运用正难则反的思想来处理,反证法就是从反面入手的一种重要的推理方法,一般地,以否定的形式出现的数学命题,我们常用反证法来实现证明。
21.解析:(Ⅰ) ,……(1分)
,……(1分)
∵函数 在
在 上单调递增,在
上单调递增,在 上单调递减,
上单调递减,
∴ 在
在 处取得极大值,有
处取得极大值,有 ,
,
 (3分)
(3分)
即 ,这就是所求的
,这就是所求的 之间的关系式.
之间的关系式.  (4分)
(4分)
(Ⅱ)当 在
在 处取得极小值,有
处取得极小值,有 ,即
,即 ,
①
,
①
又由(Ⅰ)有: ②联立①和②,解得
②联立①和②,解得 .
.
 (5分)
(5分)
此时, ,在
,在 上
上 ,
,
在 上
上 ,
,
∴ 在
在 处确可取得极小值,故
处确可取得极小值,故 ,
,  (7分)
(7分)
从而 .
.
 (8分)
(8分)
(Ⅲ)由(Ⅰ)得: ,
,
∴ ,
,
它在 上为减函数,在
上为减函数,在 为增函数.
为增函数.  (10分)
(10分)
若存在实数 ,使
,使 在
在 上为单调函数,则有
上为单调函数,则有 ,得
,得 .又因为
.又因为 ,有
,有 ,这与
,这与 矛盾.
矛盾.
所以满足题意的实数 不存在.
不存在.
 (12分)
(12分)
评析: 导数是研究函数性质的一个有力工具,运用导数求函数的单调区间和极值,可转化为解不等式 和方程
和方程 ,显得非常简捷且易于操作.值得注意的是:
,显得非常简捷且易于操作.值得注意的是: 是
是 取得极值的必要条件,因此,在(Ⅱ)中,由
取得极值的必要条件,因此,在(Ⅱ)中,由 求出
求出 ,必须检验.
,必须检验.
22.解析:(Ⅰ)由题意可得 ,
,  (2分)
(2分)
由 ,得
,得 ,∴
,∴ ,
,  (4分)
(4分)
∴椭圆 的方程为
的方程为 .
.
 (4分)
(4分)
(Ⅱ)由(Ⅰ)可得椭圆 的左焦点为
的左焦点为 ,左准线为
,左准线为 ,
,
连结 ,则
,则 ,设
,设 ,则
,则 ,
,
∴ ,
,
 (6分)
(6分)
化简得 的方程为
的方程为 .
.
 (8分)
(8分)
(Ⅲ)将曲线 向右平移2个单位,得曲线
向右平移2个单位,得曲线 的方程为:
的方程为:  ,其焦点为
,其焦点为 ,准线为
,准线为 ,对称轴为
,对称轴为 轴.
轴.  (10分)
(10分)
设直线 的方程为
的方程为 ,代入y2=4x,得y2-4ty-4=0.
,代入y2=4x,得y2-4ty-4=0.
由题意,可设 (
( ),
), (
( ),则y1y2=-4,
),则y1y2=-4,
且有
 (12分)
(12分)
∴ ,
, ,
,
得 .
.
∴ 三点共线.
三点共线.
 (14分)
(14分)
评析:证明三点共线的方法很多,这里运用向量共线定理来证,体现了平面向量与解析几何知识的交汇和平面向量知识在解析几何中的应用.近几年的高考突出了在知识网络的交汇点处设计命题的要求,平面向量与解析几何知识的综合考查成为一个不衰的热点,复习中要引起重视.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com