
题目列表(包括答案和解析)
(本小题满分14分)
如图,四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90 ,且BC=2AD=2,AB=4,SA=3.
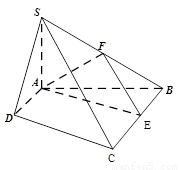
(1)求证:平面SBC⊥平面SAB;
(2)若E、F分别为线段BC、SB上的一点(端点除外),满足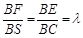 .(
.(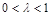 )
)
①求证:对于任意的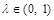 ,恒有SC∥平面AEF;
,恒有SC∥平面AEF;
②是否存在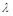 ,使得△AEF为直角三角形,若存在,求出所有符合条件的
,使得△AEF为直角三角形,若存在,求出所有符合条件的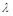 值;若不存在,说明理由.
值;若不存在,说明理由.
(本小题满分14分)
如图,四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90 ,且BC=2AD=2,AB=4,SA=3.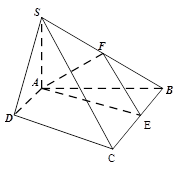
(1)求证:平面SBC⊥平面SAB;
(2)若E、F分别为线段BC、SB上的一点(端点除外),满足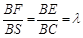 .(
.(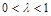 )
)
①求证:对于任意的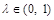 ,恒有SC∥平面AEF;
,恒有SC∥平面AEF;
②是否存在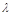 ,使得△AEF为直角三角形,若存在,求出所有符合条件的
,使得△AEF为直角三角形,若存在,求出所有符合条件的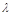 值;若不存在,说明理由.
值;若不存在,说明理由.
(本小题满分14分)
如图,四棱锥P-ABCD的底面为矩形,侧面PAD是正三角形,且侧面PAD⊥底面ABCD
(I) 求证:平面PAD⊥平面PCD
(II) 试在平面PCD上确定一点 E 的位置,使 |\S\UP6(→| 最小,并说明理由;
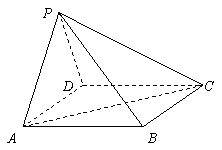 (III) 当AD = AB时,求二面角A-PC-D的余弦值.
(III) 当AD = AB时,求二面角A-PC-D的余弦值.
(本小题满分14分)
如图,四棱锥P-ABCD的底面为矩形,侧面PAD是正三角形,且侧面PAD⊥底面ABCD
(I) 求证:平面PAD⊥平面PCD
(II) 试在平面PCD上确定一点 E 的位置,使 |\S\UP6(→| 最小,并说明理由;
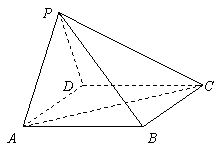 (III) 当AD = AB时,求二面角A-PC-D的余弦值.
(III) 当AD = AB时,求二面角A-PC-D的余弦值.
 倍,P为侧棱SD上的点。
倍,P为侧棱SD上的点。 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com