
(1)同解法一……………………4分
(2)∵A1B1C1―ABC为直三棱住 C1C=CB=CA=2
AC⊥CB D、E分别为C1C、B1C1的中点
建立如图所示的坐标系得
C(0,0,0) B(2,0,0) A(0,2,0)
C1(0,0,2) B1(2,0,2) A1(0,2,2)
D(0,0,1) E(1,0,2)………………6分
 设平面A1BD的法向量为n
设平面A1BD的法向量为n

 …………8分
…………8分
平面ACC1A1的法向量为m=(1,0,0)  …………9分
…………9分
即二面角B―A1D―A的大小为 ………………10分
………………10分
20.(文) 解:将各项指标合格分别记作A1,A2,A3,A4,A5,则
(1)由于“至少有两项指标不合格”,与“至多1项指标不合格”对立,故这个电子
元件不能出厂的概率为  ………………6分
………………6分
(2)直到五项指标全部检查完才能确定该元件是否出厂,表明前4项检验中恰有1项
检验不合格. 故直到五项指标全部检查完才能确定该元件是否出厂的概率为
 ……………………12分
……………………12分
(理) 解:(Ⅰ)

1
2
3
4
5
6
7
8
9
P









(Ⅱ)
21.解:(1)当k=0时,y=1与3x2-y2=1有二公共点;若k≠0,则x= (y-1)代入3x2-y2=1有(3-k2)y2-6y+3-k2=0,显然k2=3时,直线与双曲线渐近线平行,无二公共点,所以k2≠3.由y∈R,所以Δ=36-4(3-k2)2≥0,所以0<k2<6,且k2≠3.综合知k≠(-
(y-1)代入3x2-y2=1有(3-k2)y2-6y+3-k2=0,显然k2=3时,直线与双曲线渐近线平行,无二公共点,所以k2≠3.由y∈R,所以Δ=36-4(3-k2)2≥0,所以0<k2<6,且k2≠3.综合知k≠(- ,
, )且k≠±
)且k≠± 时,直线与双曲线交于二点,反之亦然.
时,直线与双曲线交于二点,反之亦然.
(2)设A(x1,y1)、B(x2,y2),消去y,得(3-k2)x2-2kx-2=0的二根为x1、x2,所以x1+x2= ,x1x2=
,x1x2= ,由(1)知y1y2=1,因为圆过原点,以AB为直径,所以x1x2+y1y2=0,所以k2=1,即k=±1为所求的值.
,由(1)知y1y2=1,因为圆过原点,以AB为直径,所以x1x2+y1y2=0,所以k2=1,即k=±1为所求的值.
22.解:(1)
 ………………2分
………………2分
由已知条件得:
 ………………4分
………………4分
(2) ………………5分
………………5分
 ………………6分
………………6分
令
 ………………7分
………………7分
∴函数 的单调递增区间为
的单调递增区间为
当 时,函数
时,函数 的单调递增区间为(0,2)…………8分
的单调递增区间为(0,2)…………8分
综上:当m>0时,函数 的单调递增区间为
的单调递增区间为 ;当
;当 时,
时,
函数 的单调递增区间为(0,2)………………9分
的单调递增区间为(0,2)………………9分
(3)由(1)得:

 …………10分
…………10分
令 ………………11分
………………11分

即: ……………………14分
……………………14分
数学2参考答案(2007年10月17日)
1―6、AABCCD 7―12、DBBDCA
13、(lg2,+∞) 14、0, 15、-1
15、-1
16、(文)-10,(理)(2-i)/3
19.解:(1)∵A1B1C1-ABC为直三棱住 ∴CC1⊥底面ABC ∴CC1⊥BC
∵AC⊥CB ∴BC⊥平面A1C1CA………………2分
∴BC长度即为B点到平面A1C1CA的距离
∵BC=2 ∴点B到平面A1C1CA的距离为2……………………4分
(2)分别延长AC,A1D交于G. 过C作CM⊥A1G 于M,连结BM
∵BC⊥平面ACC1A1 ∴CM为BM在平面A1C1CA的内射影
∴BM⊥A1G ∴∠CMB为二面角B―A1D―A的平面角 ……………………6分
平面A1C1CA中,C1C=CA=2,D为C1C的中点
∴CG=2,DC=1 在直角三角形CDG中, 
 ……9分
……9分
即二面角B―A1D―A的大小为 ………………10分
………………10分

(1)同解法一……………………4分 (2)∵A1B1C1―ABC为直三棱住 C1C=CB=CA=2 AC⊥CB D、E分别为C1C、B1C1的中点 建立如图所示的坐标系得 C(0,0,0) B(2,0,0) A(0,2,0) C1(0,0,2) B1(2,0,2) A1(0,2,2) D(0,0,1) E(1,0,2)………………6分  设平面A1BD的法向量为n 设平面A1BD的法向量为n
  …………8分 …………8分
平面ACC1A1的法向量为m=(1,0,0)  …………9分 …………9分 即二面角B―A1D―A的大小为 ………………10分 ………………10分 20.(文) 解:将各项指标合格分别记作A1,A2,A3,A4,A5,则 (1)由于“至少有两项指标不合格”,与“至多1项指标不合格”对立,故这个电子 元件不能出厂的概率为  ………………6分 ………………6分 (2)直到五项指标全部检查完才能确定该元件是否出厂,表明前4项检验中恰有1项 检验不合格. 故直到五项指标全部检查完才能确定该元件是否出厂的概率为  ……………………12分 ……………………12分
(理) 解:(Ⅰ) 
1 2 3 4 5 6 7 8 9 P 








(Ⅱ) 21.解:(1)当k=0时,y=1与3x2-y2=1有二公共点;若k≠0,则x= (y-1)代入3x2-y2=1有(3-k2)y2-6y+3-k2=0,显然k2=3时,直线与双曲线渐近线平行,无二公共点,所以k2≠3.由y∈R,所以Δ=36-4(3-k2)2≥0,所以0<k2<6,且k2≠3.综合知k≠(- (y-1)代入3x2-y2=1有(3-k2)y2-6y+3-k2=0,显然k2=3时,直线与双曲线渐近线平行,无二公共点,所以k2≠3.由y∈R,所以Δ=36-4(3-k2)2≥0,所以0<k2<6,且k2≠3.综合知k≠(- , , )且k≠± )且k≠± 时,直线与双曲线交于二点,反之亦然. 时,直线与双曲线交于二点,反之亦然. (2)设A(x1,y1)、B(x2,y2),消去y,得(3-k2)x2-2kx-2=0的二根为x1、x2,所以x1+x2= ,x1x2= ,x1x2= ,由(1)知y1y2=1,因为圆过原点,以AB为直径,所以x1x2+y1y2=0,所以k2=1,即k=±1为所求的值. ,由(1)知y1y2=1,因为圆过原点,以AB为直径,所以x1x2+y1y2=0,所以k2=1,即k=±1为所求的值. 22.解:(1)  ………………2分 ………………2分 由已知条件得:  ………………4分 ………………4分 (2) ………………5分 ………………5分  ………………6分 ………………6分 令  ………………7分 ………………7分 ∴函数 的单调递增区间为 的单调递增区间为 当 时,函数 时,函数 的单调递增区间为(0,2)…………8分 的单调递增区间为(0,2)…………8分 综上:当m>0时,函数 的单调递增区间为 的单调递增区间为 ;当 ;当 时, 时, 函数 的单调递增区间为(0,2)………………9分 的单调递增区间为(0,2)………………9分 (3)由(1)得:   …………10分 …………10分 令 ………………11分 ………………11分  即: ……………………14分 ……………………14分
| |

 的值为( )
的值为( )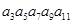 =243,则
=243,则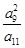 的值为( )
的值为( )![]() 的值为
的值为![]() 的值为
的值为 15、-1
15、-1
 ……9分
……9分 ………………10分
………………10分