
题目列表(包括答案和解析)
(本小题满分1 0分)
如图,已知线段AB∥CD,AD与B C相交于点K,E是线段AD上一动点。
【小题1】(1)若BK= KC,求
KC,求 的值;
的值;
【小题2】(2)连接BE,若BE平分∠ABC,则当AE=  AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明.再探究:当AE=
AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明.再探究:当AE= AD (n>2),而其余条件不变时,线段AB、BC、CD三者之间又有怎样的等量关系?请直接写出你的结论,不必证明.
AD (n>2),而其余条件不变时,线段AB、BC、CD三者之间又有怎样的等量关系?请直接写出你的结论,不必证明.

 ;
;
 以上观察探究,请你总结中点四边形的形状由原四边形的什么决定的?
以上观察探究,请你总结中点四边形的形状由原四边形的什么决定的?(本小题满分10分)
观察控究,完成证明和填空.
如图,四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,顺次连接E、F、G、H,得到的四边形EFGH叫中点四边形.
【小题1】(1)求证:四边形EFGH是平行四边形 ;
;
【小题2】(2)如图,当四边形ABCD变成等腰梯形时,它的中点四边形是菱形,请你探究并填空: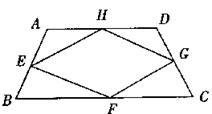
当四边形ABCD变成平行四边形时,它的中点四边形是__________;
当四边形ABCD变成矩形时,它的中点四边形是__________;
当四边形ABCD变成菱形时,它的中点四边形是__________;
当四边形ABCD变成正方形时,它的中点四边形是__________;
【小题3】(3)根据 以上观察探究,请你总结中点四边形的形状由原四边形的什么决定的?
以上观察探究,请你总结中点四边形的形状由原四边形的什么决定的?
(本小题满分10分)
观察控究,完成证明和填空.
如图,四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,顺次连接E、F、G、H,得到的四边形EFGH叫中点四边形.

1.(1)求证:四边形EFGH是平行四边形;
2.(2)如图,当四边形ABCD变成等腰梯形时,它的中点四边形是菱形,请你探究并填空:

当四边形ABCD变成平行四边形时,它的中点四边形是__________;
当四边形ABCD变成矩形时,它的中点四边形是__________;
当四边形ABCD变成菱形时,它的中点四边形是__________;
当四边形ABCD变成正方形时,它的中点四边形是__________;
3.(3)根据以上观察探究,请你总结中点四边形的形状由原四边形的什么决定的?
(本小题满分10分)
观察控究,完成证明和填空.
如图,四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,顺次连接E、F、G、H,得到的四边形EFGH叫中点四边形.

1.(1)求证:四边形EFGH是平行四边形;
2.(2)如图,当四边形ABCD变成等腰梯形时,它的中点四边形是菱形,请你探究并填空:

当四边形ABCD变成平行四边形时,它的中点四边形是__________;
当四边形ABCD变成矩形时,它的中点四边形是__________;
当四边形ABCD变成菱形时,它的中点四边形是__________;
当四边形ABCD变成正方形时,它的中点四边形是__________;
3.(3)根据以上观察探究,请你总结中点四边形的形状由原四边形的什么决定的?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com