
题目列表(包括答案和解析)
若不等式组 (其中
(其中 )表示的平面区域的面积是9.
)表示的平面区域的面积是9.
(1)求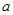 的值;(2)求
的值;(2)求 的最小值,及此时
的最小值,及此时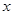 与
与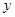 的值.
的值.
 (其中
(其中 )表示的平面区域的面积是9.
)表示的平面区域的面积是9. 的值;(2)求
的值;(2)求 的最小值,及此时
的最小值,及此时 与
与 的值.
的值.探究函数![]() ,x∈(0,+∞)的最小值,并确定相应的x的值,列表如下:
,x∈(0,+∞)的最小值,并确定相应的x的值,列表如下:
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.102 | 4.24 | 4.3 | 5 | 5.8 | 7.57 | … |
请观察表中y值随x值变化的特点,完成下列问题:
(1)若函数![]() ,(x>0)在区间(0,2)上递减,则在 上递增;
,(x>0)在区间(0,2)上递减,则在 上递增;
(2)当x= 时,![]() ,(x>0)的最小值为 ;
,(x>0)的最小值为 ;
(3)试用定义证明![]() ,(x>0)在区间(0,2)上递减;
,(x>0)在区间(0,2)上递减;
(4)函数![]() ,(x<0)有最值吗?是最大值还是最小值?此时x为何值?
,(x<0)有最值吗?是最大值还是最小值?此时x为何值?
(5)解不等式![]() .
.
解题说明:(1)(2)两题的结果直接填写在横线上;(4)题直接回答,不需证明。
 成立,则n的最小值是( )
成立,则n的最小值是( ) 成立,则n的最小值是( )
成立,则n的最小值是( )
一、选择题
1―5 CADBA 6―10 CBABD 11―12 CC
二、填空题
13.(理) (文)(―1,1) 14.
(文)(―1,1) 14. 15.(理)18(文)(1,0)
15.(理)18(文)(1,0)
16.①③
三、解答题
17.解:(1)由题意得 ………………2分
………………2分

(2)由 可知A、B都是锐角, …………7分
可知A、B都是锐角, …………7分

这时三角形为有一顶角为120°的等腰三角形 …………12分
18.(理)解:(1)ξ的所有可能的取值为0,1,2,3。 ………………2分

(2) ………………12分
………………12分
(文)解:(1) ; ………………6分
; ………………6分
(2)因为
 …………10分
…………10分
所以 …………12分
…………12分
19.解:(1) , ………………1分
, ………………1分
依题意知, ………………3分
………………3分
(2)令 …………4分
…………4分
 …………5分
…………5分
所以, …………7分
…………7分
(3)由上可知
①当 恒成立,
恒成立,
必须且只须 , …………8分
, …………8分
 ,
,
则 ………………9分
………………9分
②当 ……10分
……10分
要使当
综上所述,t的取值范围是 ………………12分
………………12分
20.解法一:(1)取BB1的中点D,连CD、AD,则∠ACD为所求。…………1分

(2)方法一 作CE⊥AB于E,C1E1⊥A1B1于E1,连EE1,
则AB⊥面CC1E1E,因此平面PAB⊥面CC1E1E。
因为A1B1//AB,所以A1B1//平面PAB。则只需求点E1到平面PAB的距离。
作E1H⊥EP于H,则E1H⊥平面PAB,则E1H即为所求距离。 …………6分
求得 …………8分
…………8分
方法二:设B1到平面PAB的距离为h,则由
得 ………………8分
………………8分
(3)设平面PAB与平面PA1B1的交线为l,由(2)知,A1B1//平面PAB,
则A1B1//l,因为AB⊥面CC1E1E,则l⊥面CC1E1E,
所以∠EPE1就是二面有AB―P―A1B的平面角。 ………………9分
要使平面PAB⊥平面PA1B1,只需∠EPE1=90°。 ………………10分
在矩形CEE1C1中,
解得
|