
题目列表(包括答案和解析)

| L |
| t1 |
| L |
| t1 |
| L |
| t2 |
| L |
| t2 |
| 次 数 |
滑块1 | 滑块2 | 碰前系统动量kgms-1 | 碰后系统动量kgms-1 | |||
| v1/ms-1 | v/ms-1 | v2/ms-1 | v/ms-1 | m1v1 | m2v2 | (m1+m2)v | |
| 1 | 0.290 | 0.184 | 0 | 0.184 | 0.0940 0.0940 |
0 | 0.0929 0.0929 |
| 2 | 0.426 | 0.269 | 0 | 0.269 | 0.138 0.138 |
0 | 0.136 0.136 |
| 实验结论: 在误差允许范围内,系统碰撞前后动量矢量和相等,即系统动量守恒 在误差允许范围内,系统碰撞前后动量矢量和相等,即系统动量守恒 | |||||||
| L |
| t1 |
| L |
| t2 |
| L |
| t1 |
| L |
| t2 |
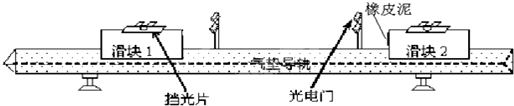
| 次 数 |
滑块1 | 滑块2 | 碰前系统动量kgms-1 | 碰后系统动量kgms-1 | |||
| v1/ms-1 | v/ms-1 | v2/ms-1 | v/ms-1 | m1v1 | m2v2 | (m1+m2)v | |
| 1 | 0.290 | 0.184 | 0 | 0.184 | ______ | 0 | ______ |
| 2 | 0.426 | 0.269 | 0 | 0.269 | ______ | 0 | ______ |
| 实验结论:______ | |||||||
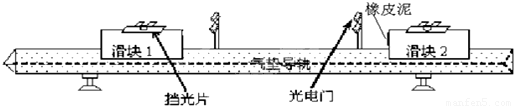
| 次 数 | 滑块1 | 滑块2 | 碰前系统动量kgms-1 | 碰后系统动量kgms-1 | |||
| v1/ms-1 | v/ms-1 | v2/ms-1 | v/ms-1 | m1v1 | m2v2 | (m1+m2)v | |
| 1 | 0.290 | 0.184 | 0.184 | ||||
| 2 | 0.426 | 0.269 | 0.269 | ||||
| 实验结论: | |||||||
第七部分 热学
热学知识在奥赛中的要求不以深度见长,但知识点却非常地多(考纲中罗列的知识点几乎和整个力学——前五部分——的知识点数目相等)。而且,由于高考要求对热学的要求逐年降低(本届尤其低得“离谱”,连理想气体状态方程都没有了),这就客观上给奥赛培训增加了负担。因此,本部分只能采新授课的培训模式,将知识点和例题讲解及时地结合,争取让学员学一点,就领会一点、巩固一点,然后再层叠式地往前推进。
一、分子动理论
1、物质是由大量分子组成的(注意分子体积和分子所占据空间的区别)
对于分子(单原子分子)间距的计算,气体和液体可直接用![]() ,对固体,则与分子的空间排列(晶体的点阵)有关。
,对固体,则与分子的空间排列(晶体的点阵)有关。

【例题1】如图6-1所示,食盐(NaCl)的晶体是由钠离子(图中的白色圆点表示)和氯离子(图中的黑色圆点表示)组成的,离子键两两垂直且键长相等。已知食盐的摩尔质量为58.5×10-3kg/mol,密度为2.2×103kg/m3,阿伏加德罗常数为6.0×1023mol-1,求食盐晶体中两个距离最近的钠离子中心之间的距离。
【解说】题意所求即图中任意一个小立方块的变长(设为a)的![]() 倍,所以求a成为本题的焦点。
倍,所以求a成为本题的焦点。
由于一摩尔的氯化钠含有NA个氯化钠分子,事实上也含有2NA个钠离子(或氯离子),所以每个钠离子占据空间为 v = ![]()
而由图不难看出,一个离子占据的空间就是小立方体的体积a3 ,
即 a3 = ![]() =
= ![]() ,最后,邻近钠离子之间的距离l =
,最后,邻近钠离子之间的距离l = ![]() a
a
【答案】3.97×10-10m 。
〖思考〗本题还有没有其它思路?
〖答案〗每个离子都被八个小立方体均分,故一个小立方体含有![]() ×8个离子 =
×8个离子 = ![]() 分子,所以…(此法普遍适用于空间点阵比较复杂的晶体结构。)
分子,所以…(此法普遍适用于空间点阵比较复杂的晶体结构。)
2、物质内的分子永不停息地作无规则运动
固体分子在平衡位置附近做微小振动(振幅数量级为0.1![]() ),少数可以脱离平衡位置运动。液体分子的运动则可以用“长时间的定居(振动)和短时间的迁移”来概括,这是由于液体分子间距较固体大的结果。气体分子基本“居无定所”,不停地迁移(常温下,速率数量级为102m/s)。
),少数可以脱离平衡位置运动。液体分子的运动则可以用“长时间的定居(振动)和短时间的迁移”来概括,这是由于液体分子间距较固体大的结果。气体分子基本“居无定所”,不停地迁移(常温下,速率数量级为102m/s)。
无论是振动还是迁移,都具备两个特点:a、偶然无序(杂乱无章)和统计有序(分子数比率和速率对应一定的规律——如麦克斯韦速率分布函数,如图6-2所示);b、剧烈程度和温度相关。

气体分子的三种速率。最可几速率vP :f(v) = ![]() (其中ΔN表示v到v +Δv内分子数,N表示分子总数)极大时的速率,vP =
(其中ΔN表示v到v +Δv内分子数,N表示分子总数)极大时的速率,vP =![]() =
=![]() ;平均速率
;平均速率![]() :所有分子速率的算术平均值,
:所有分子速率的算术平均值,![]() =
=![]() =
=![]() ;方均根速率
;方均根速率![]() :与分子平均动能密切相关的一个速率,
:与分子平均动能密切相关的一个速率,![]() =
=![]() =
=![]() 〔其中R为普适气体恒量,R = 8.31J/(mol.K)。k为玻耳兹曼常量,k =
〔其中R为普适气体恒量,R = 8.31J/(mol.K)。k为玻耳兹曼常量,k = ![]() = 1.38×10-23J/K 〕
= 1.38×10-23J/K 〕
【例题2】证明理想气体的压强P = ![]() n
n![]() ,其中n为分子数密度,
,其中n为分子数密度,![]() 为气体分子平均动能。
为气体分子平均动能。

【证明】气体的压强即单位面积容器壁所承受的分子的撞击力,这里可以设理想气体被封闭在一个边长为a的立方体容器中,如图6-3所示。
考查yoz平面的一个容器壁,P = ![]() ①
①
设想在Δt时间内,有Nx个分子(设质量为m)沿x方向以恒定的速率vx碰撞该容器壁,且碰后原速率弹回,则根据动量定理,容器壁承受的压力
F =![]() =
=![]() ②
②
在气体的实际状况中,如何寻求Nx和vx呢?
考查某一个分子的运动,设它的速度为v ,它沿x、y、z三个方向分解后,满足
v2 = ![]() +
+ ![]() +
+ ![]()
分子运动虽然是杂乱无章的,但仍具有“偶然无序和统计有序”的规律,即
![]() =
= ![]() +
+ ![]() +
+ ![]() = 3
= 3![]() ③
③
这就解决了vx的问题。另外,从速度的分解不难理解,每一个分子都有机会均等的碰撞3个容器壁的可能。设Δt = ![]() ,则
,则
Nx = ![]() ·3N总 =
·3N总 = ![]() na3 ④
na3 ④
注意,这里的![]() 是指有6个容器壁需要碰撞,而它们被碰的几率是均等的。
是指有6个容器壁需要碰撞,而它们被碰的几率是均等的。

结合①②③④式不难证明题设结论。
〖思考〗此题有没有更简便的处理方法?
〖答案〗有。“命令”所有分子以相同的速率v沿+x、?x、+y、?y、+z、?z这6个方向运动(这样造成的宏观效果和“杂乱无章”地运动时是一样的),则 Nx =![]() N总 =
N总 = ![]() na3 ;而且vx = v
na3 ;而且vx = v
所以,P = ![]() =
= ![]() =
= =
=![]() nm
nm![]() =
= ![]() n
n![]()
3、分子间存在相互作用力(注意分子斥力和气体分子碰撞作用力的区别),而且引力和斥力同时存在,宏观上感受到的是其合效果。
分子力是保守力,分子间距改变时,分子力做的功可以用分子势能的变化表示,分子势能EP随分子间距的变化关系如图6-4所示。
分子势能和动能的总和称为物体的内能。
二、热现象和基本热力学定律
1、平衡态、状态参量
a、凡是与温度有关的现象均称为热现象,热学是研究热现象的科学。热学研究的对象都是有大量分子组成的宏观物体,通称为热力学系统(简称系统)。当系统的宏观性质不再随时间变化时,这样的状态称为平衡态。
b、系统处于平衡态时,所有宏观量都具有确定的值,这些确定的值称为状态参量(描述气体的状态参量就是P、V和T)。
c、热力学第零定律(温度存在定律):若两个热力学系统中的任何一个系统都和第三个热力学系统处于热平衡状态,那么,这两个热力学系统也必定处于热平衡。这个定律反映出:处在同一热平衡状态的所有的热力学系统都具有一个共同的宏观特征,这一特征是由这些互为热平衡系统的状态所决定的一个数值相等的状态函数,这个状态函数被定义为温度。
2、温度
a、温度即物体的冷热程度,温度的数值表示法称为温标。典型的温标有摄氏温标t、华氏温标F(F = ![]() t + 32)和热力学温标T(T = t + 273.15)。
t + 32)和热力学温标T(T = t + 273.15)。
b、(理想)气体温度的微观解释:![]() =
= ![]() kT (i为分子的自由度 = 平动自由度t + 转动自由度r + 振动自由度s 。对单原子分子i = 3 ,“刚性”〈忽略振动,s = 0,但r = 2〉双原子分子i = 5 。对于三个或三个以上的多原子分子,i = 6 。能量按自由度是均分的),所以说温度是物质分子平均动能的标志。
kT (i为分子的自由度 = 平动自由度t + 转动自由度r + 振动自由度s 。对单原子分子i = 3 ,“刚性”〈忽略振动,s = 0,但r = 2〉双原子分子i = 5 。对于三个或三个以上的多原子分子,i = 6 。能量按自由度是均分的),所以说温度是物质分子平均动能的标志。
c、热力学第三定律:热力学零度不可能达到。(结合分子动理论的观点2和温度的微观解释很好理解。)
3、热力学过程
a、热传递。热传递有三种方式:传导(对长L、横截面积S的柱体,Q = K![]() SΔ
SΔ
富兰克林(Benjamin Franklin,1706-1790年)美国科学家、物理学家、发明家、政治家、社会活动家.1706年1月27日生于波士顿一个工人家庭.父亲是英国移民,从事肥皂和蜡烛制造.由于家庭贫寒,从8岁起只上了两年学就辍学当了学徒,从12岁起在他大哥的印刷所里当学徒,以后长期从事印刷工作.他刻苦自学,他说:“读书是我唯一的娱乐.”他常常去找别人或书店借书,利用深夜读书,清晨就去归还.他曾以笔名Richard Saunders投稿,报纸编辑以为文章“出自名家手笔”.他不仅从书本上学习各种知识,还辗转到纽约、伦敦、费城等地流浪,在社会生活中学习.21岁时,他在费城创办了北美第一个青年自学团体“共读社”,组织工人、技师、鞋匠、瓦匠、诗人等每周星期五来讨论哲学、科学、技术、文艺问题.这个团体后来发展为1743年创立的美利坚哲学会.1769年他被选为该会的会长.25岁时他又在费城创办了北美第一个公共图书馆,以后发展为北美公共图书馆.45岁时,他又创办费城学院(即后来的宾夕法尼亚大学).
富兰克林在电学上有许多重要贡献.通过实验,他对当时许多混乱的电学知识(如电的产生、转移、感应、存储、充放电等)作了比较系统的清理.他曾把多个莱顿瓶连结起来,储存更多电荷.他用实验证明莱顿瓶内外金属箔所带电荷数量相等,电性相反.1747年5月25日他在给柯林森的信中,提出了电的单流质理论,并用数学上的正负来表示多余或缺少这种电流质.他还认为摩擦起电只是使电荷转移而不是创生,所生电荷的正负必须严格相等——这个思想后来发展为电学中的基本定律之一——电荷守恒定律.他利用这一理论说明了带介质的电容器原理.
富兰克林的第二项重大贡献是统一了天电和地电,彻底破除了人们对雷电的恐惧.1749年,他的夫人丽达在观看莱顿瓶串联实验时,无意碰到莱顿瓶上的金属杆,被电火花击倒在地,卧病一周,使他更坚定了探讨雷电实质的决心.他一方面列举了12条静电火花与雷电火花的相同之处,一方面通过岗亭实验和风筝实验(1752年6月)给予实验证明.他的一封封书信通过柯林森在英国皇家学会宣读,开始时受到的是嘲笑、怀疑,后来他的论文集《电学实验与研究》出版,特别是风筝实验的报告轰动了欧洲,使人们看到电学是一门有广大前景的科学,避雷针也成了人类破除迷信征服自然的一项重要技术成果,推动了电学、电工学的发展.
思考:人穷志不穷,逆境成就英雄.命运把握在自己手中,就看你怎么对待它.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com