
题目列表(包括答案和解析)
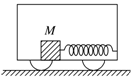

图15
(1)给出细绳被拉断的条件.
(2)长滑块在细绳拉断后被加速的过程中,所能获得的最大向左的加速度为多大?
(3)小物体最后离开长滑块时,相对地面速度恰好为零的条件是什么?
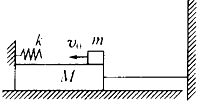 如图所示,质量为M的长滑块静止在光滑水平面上,左侧固定一劲度系数k足够大的水平轻质弹簧,右侧用一不可伸长的细轻绳连接于竖直墙上,细绳所能承受的最大拉力为T.使一质量为m、初速度为v0的小物块,在滑块上无摩擦地向左滑动,而后压缩弹簧.(弹簧弹性势能的表达式Ep=
如图所示,质量为M的长滑块静止在光滑水平面上,左侧固定一劲度系数k足够大的水平轻质弹簧,右侧用一不可伸长的细轻绳连接于竖直墙上,细绳所能承受的最大拉力为T.使一质量为m、初速度为v0的小物块,在滑块上无摩擦地向左滑动,而后压缩弹簧.(弹簧弹性势能的表达式Ep=| 1 |
| 2 |
| T | ||
|
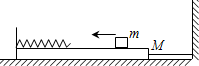 如图所示,质量为M的长方形木板静止在光滑水平面上,木板的左侧固定一劲度系数为k的轻质弹簧,木板的右侧用一根伸直的并且不可伸长的轻绳水平地连接在竖直墙上.绳所能承受的最大拉力为T.一质量为m的小滑块以一定的速度在木板上无摩擦地向左运动,而后压缩弹簧.弹簧被压缩后所获得的弹性势能可用公式EP=
如图所示,质量为M的长方形木板静止在光滑水平面上,木板的左侧固定一劲度系数为k的轻质弹簧,木板的右侧用一根伸直的并且不可伸长的轻绳水平地连接在竖直墙上.绳所能承受的最大拉力为T.一质量为m的小滑块以一定的速度在木板上无摩擦地向左运动,而后压缩弹簧.弹簧被压缩后所获得的弹性势能可用公式EP=| 1 | 2 |
| 1 | 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com