
题目列表(包括答案和解析)
在一段时间内,某种商品价格x(万元)和需求量Y(t)之间的一组数据为
价 格x:1.4 1.6 1.8 2 2.2
需求量Y:12 10 7 5 3
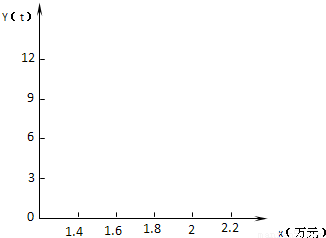
(1)画出散点图;
(2)求出Y对x的回归直线方程,并在(1)的散点图中画出它的图象;
(3)如价格定为1.9万元,预测需求量大约是多少(精确到0.01 t)?
价 格x:1.4 1.6 1.8 2 2.2
需求量Y:12 10 7 5 13 3
(1)画出散点图;
(2)求出Y对x的回归直线方程,并在(1)的散点图中画出它的图象;
(3)如价格定为1.9万元,预测需求量大约是多少(精确到0.01 t)?
| 价格x | 1.4 | 1.6 | 1.8 | 2 | 2.2 |
| 需求量Y | 12 | 10 | 7 | 5 | 3 |

 |
| y |
 |
| a |
 |
| b |
 |
| b |
| |||||||
|
 |
| a |
. |
| y |
 |
| b |
. |
| x |
| 序号 | ||||
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 求和 |
| 价格x | 1.4 | 1.6 | 1.8 | 2 | 2.2 |
| 需求量Y | 12 | 10 | 7 | 5 | 3 |
 =
= ;(其中:
;(其中: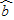 =
= ,
,
| 序号 | ||||
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 求和 |
| 价格x | 1.4 | 1.6 | 1.8 | 2 | 2.2 |
| 需求量Y | 12 | 10 | 7 | 5 | 3 |

 =
= ;(其中:
;(其中: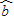 =
=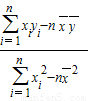 ,
,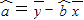
| 序号 | ||||
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 求和 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com