
题目列表(包括答案和解析)
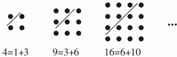 14、古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16…这样的数称为“正方形数”.如图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形”之和,下列等式中,符合这一规律的表达式是
14、古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16…这样的数称为“正方形数”.如图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形”之和,下列等式中,符合这一规律的表达式是古希腊著名的毕达哥拉斯学派把1、3、6、10 这样的数称为“三角形数”,而把1、4、9、16 这样的数称为“正方形数”.如图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和,下列等式中,符合这一规律的表达式是
①13=3+10; ②25=9+16 ③36=15+21; ④49=18+31;⑤64=28+36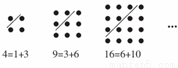
古希腊著名的毕达哥拉斯学派把1、3、6、10  这样的数称为“”,
这样的数称为“”,
而把1、4、9、16 这样的数称为“正方形数”.如图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )
这样的数称为“正方形数”.如图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )
A.13 = 3+10 B. 36 = 15+21 C. 25 = 9+16 D.49= 18+31
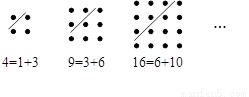
古希腊著名的毕达哥拉斯学派把1、3、6、10……这样的数称为“三角形数”,而把1、4、9、16……这样的数称为“正方形数”。如图可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形”之和,下列等式中,符合这一规律的表达式为 ▲

①13=3+10; ②25=9+16; ③36=15+21; ④49=18+31; ⑤64=28+36
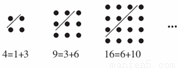
古希腊著名的毕达哥拉斯学派把1、3、6、10……这样的数称为“三角形数”,而把1、4、9、16……这样 的数称为“正方形数”.如图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和,下列等式中,符合这一规律的表达式是
①13=3+10; ②25=9+16 ③36=15+21; ④49=18+31; ⑤64=28+36
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com