
题目列表(包括答案和解析)
已知函数 
 R).
R).
(Ⅰ)若  ,求曲线
,求曲线
 在点
在点  处的的切线方程;
处的的切线方程;
(Ⅱ)若  对任意
对任意 
 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【解析】本试题主要考查了导数在研究函数中的运用。
第一问中,利用当 时,
时, .
.
 因为切点为(
因为切点为( ),
则
),
则 ,
,
所以在点( )处的曲线的切线方程为:
)处的曲线的切线方程为:
第二问中,由题意得, 即
即 即可。
即可。
Ⅰ)当 时,
时, .
.
 ,
,
因为切点为( ),
则
),
则 ,
,
所以在点( )处的曲线的切线方程为:
)处的曲线的切线方程为: . ……5分
. ……5分
(Ⅱ)解法一:由题意得, 即
即 . ……9分
. ……9分
(注:凡代入特殊值缩小范围的均给4分)
 ,
,
因为 ,所以
,所以 恒成立,
恒成立,
故 在
在 上单调递增,
……12分
上单调递增,
……12分
要使 恒成立,则
恒成立,则 ,解得
,解得 .……15分
.……15分
解法二: ……7分
……7分
(1)当 时,
时, 在
在 上恒成立,
上恒成立,
故 在
在 上单调递增,
上单调递增,
 即
即 .
……10分
.
……10分
(2)当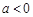 时,令
时,令 ,对称轴
,对称轴 ,
,
则 在
在 上单调递增,又
上单调递增,又
① 当 ,即
,即 时,
时, 在
在 上恒成立,
上恒成立,
所以 在
在 单调递增,
单调递增,
 即
即 ,不合题意,舍去
,不合题意,舍去
②当 时,
时, ,
不合题意,舍去 14分
,
不合题意,舍去 14分
综上所述:
在△ABC中,内角A、B、C所对边的边长分别是a、b、c,已知c=2,C= .
.
(Ⅰ)若△ABC的面积等于 ,求a、b;
,求a、b;
(Ⅱ)若 ,求△ABC的面积.
,求△ABC的面积.
【解析】第一问中利用余弦定理及已知条件得 又因为△ABC的面积等于
又因为△ABC的面积等于 ,所以
,所以 ,得
,得 联立方程,解方程组得
联立方程,解方程组得 .
.
第二问中。由于 即为即
即为即 .
.
当 时,
时,
 ,
,  ,
,  ,
,
 所以
所以 当
当 时,得
时,得 ,由正弦定理得
,由正弦定理得 ,联立方程组
,联立方程组 ,解得
,解得 ,得到
,得到 。
。
解:(Ⅰ) (Ⅰ)由余弦定理及已知条件得 ,………1分
,………1分
又因为△ABC的面积等于 ,所以
,所以 ,得
,得 ,………1分
,………1分
联立方程,解方程组得 .
……………2分
.
……………2分
(Ⅱ)由题意得
 ,
,
即 .
…………2分
.
…………2分
当 时,
时,
 ,
,  ,
,  ,
,
 ……1分
……1分
所以 ………………1分
………………1分
当 时,得
时,得 ,由正弦定理得
,由正弦定理得 ,联立方程组
,联立方程组
 ,解得
,解得 ,
, ;
所以
;
所以
等比数列{an}的前n项和为Sn,若S3+3S2=0,则公比q=_______
【解析】显然公比 ,设首项为
,设首项为 ,则由
,则由 ,得
,得 ,即
,即 ,即
,即 ,即
,即 ,所以
,所以 ,解得
,解得 .
.
| 10-x |
| 10+x |
| 10-x |
| 10+x |
| k |
| x+a |
| x+b |
| x+c |
| 1 |
| 3 |
| 1 |
| 2 |
| kx |
| ax+1 |
| bx+1 |
| cx+1 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com