
题目列表(包括答案和解析)
已知函数![]() 的定义域为
的定义域为![]() 且
且![]() ,对任意
,对任意![]() 都有
都有![]()
![]()
数列![]() 满足
满足![]() N
N![]() .证明函数
.证明函数![]() 是奇函数;求数列
是奇函数;求数列![]() 的通项公式;令
的通项公式;令![]() N
N![]() , 证明:当
, 证明:当![]() 时,
时,![]() .
.
(本小题主要考查函数、数列、不等式等知识, 考查化归与转化、分类与整合的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力和创新意识)
(1) 写出y与x之间的函数关系式;
(2) 为使该村的人均产值年年都有增长,那么该村每年人口的净增不能超过多少人?
本小题主要考查函数知识、函数的单调性,考查数学建模,运用所学知识解决实际问题的能力.
沿海地区某农村在2002年底共有人口1480人,全年工农业生产总值为3180万元.从2003年起计划10年内该村的总产值每年增加60万元,人口每年净增A人,设从2003年起计划10内该村的总产值每年增加60万元,人口每年净增A人,设从2003年起的第x年(2003年为第一年)该村人均产值为y万元.
(1) 写出y与x之间的函数关系式;
(2) 为使该村的人均产值年年都有增长,那么该村每年人口的净增不能超过多少人?
本小题主要考查函数知识、函数的单调性,考查数学建模,运用所学知识解决实际问题的能力.
(本小题满分13分)
已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点。
(1)求椭圆C的方程;
(2)是否存在平行于OA的直线![]() ,使得直线
,使得直线![]() 与椭圆C有公共点,且直线OA与
与椭圆C有公共点,且直线OA与![]() 的距离等于4?若存在,求出直线
的距离等于4?若存在,求出直线![]() 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
【命题意图】本小题主要考查直线、椭圆等基础知识,考查运算求解能力、推理论证能力,考查函数与方程思想、数形结合思想、化归与转化思想。
已知函数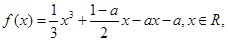 其中a>0.
其中a>0.
(I)求函数f(x)的单调区间;
(II)若函数f(x)在区间(-2,0)内恰有两个零点,求a的取值范围;
(III)当a=1时,设函数f(x)在区间[t,t+3]上的最大值为M(t),最小值为m(t),记g(t)=M(t)-m(t),求函数g(t)在区间[-3,-1]上的最小值。
【考点定位】本小题主要考查导数的运算,利用导数研究函数的单调性、函数的零点,函数的最值等基础知识.考查函数思想、分类讨论思想.考查综合分析和解决问题的能力.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com