
题目列表(包括答案和解析)
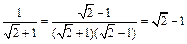 ; ②
; ②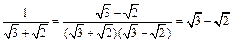 ;③
;③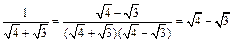 ;……
;……

(10分)观察下列等式:
① ; ②
; ② ;③
;③ ;……
;……
回答下列问题:
【小题1】(1)利用你观察到的规律,化简:
【小题2】(2)计算:
 附加题:
附加题:| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2006×2007 |
| 2006 |
| 2007 |
| 2006 |
| 2007 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 99 |
| 1 |
| 98 |
| 1 |
| 100 |
| 1 |
| 99 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 4 |
| 3 |
| 4 |
| 3 |
| 5 |
| 4 |
| 5 |
| 4 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com