甲船从A港出发顺流匀速驶向B港，行至某处，发现船上一救生圈不知何时落入水中，立刻原路返回，找到救生圈后，继续顺流驶向B港．乙船从B港出发逆流匀速驶向A港．已知救生圈漂流的速度和水流速度相同；甲、乙两船在静水中的速度相同．甲、乙两船到A港的距离y₁、y₂（km）与行驶时间x（h）之间的函数图象如图所示．

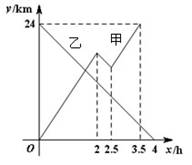
（1）写出乙船在逆流中行驶的速度（2）求甲船在逆流中行驶的路程．

（3）求甲船到A港的距离y₁与行驶时间x之间的函数关系式

（4）求救生圈落入水中时，甲船到A港的距离．

【参考公式：船顺流航行的速度船在静水中航行的速度＋水流速度，船逆流航行的速度船在静水中航行的速度水流速度．】

【解析】（1）由图可知，乙在4小时内走了24千米，根据路程=速度×时间，可得出其速度．

（2）由图可知2到2.5小时的过程中甲是逆流而行，这0.5小时内甲的速度何乙的速度相同，因此可得出甲走的路程

（3）要求距离首先要求出顺流的速度，可根据甲在0至2小时走的路程-2至2.5小时的路程+2.5至3.5小时的路程=24千米，求出顺流的速度，然后根据不同的x的范围，用待定系数法求出y与x的函数关系式．

（4）根据（3）求出的顺流的速度可求出水流的速度，然后根据船追救生圈的距离+救生圈顺水的距离=二者在掉落时间到追及时间拉开的距离．求出自变量的值，进而求出甲船到A港的距离．

甲船从A港出发顺流匀速驶向B港，行至某处，发现船上一救生圈不知何时落入水中，立刻原路返回，找到救生圈后，继续顺流驶向B港．乙船从B港出发逆流匀速驶向A港．已知救生圈漂流的速度和水流速度相同；甲、乙两船在静水中的速度相同．甲、乙两船到A港的距离y₁、y₂（km）与行驶时间x（h）之间的函数图象如图所示．

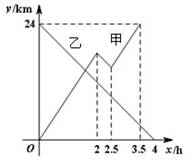
（1）写出乙船在逆流中行驶的速度（2）求甲船在逆流中行驶的路程．

（3）求甲船到A港的距离y₁与行驶时间x之间的函数关系式

（4）求救生圈落入水中时，甲船到A港的距离．

【参考公式：船顺流航行的速度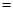船在静水中航行的速度＋水流速度，船逆流航行的速度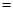船在静水中航行的速度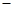水流速度．】

【解析】（1）由图可知，乙在4小时内走了24千米，根据路程=速度×时间，可得出其速度．

（2）由图可知2到2.5小时的过程中甲是逆流而行，这0.5小时内甲的速度何乙的速度相同，因此可得出甲走的路程

（3）要求距离首先要求出顺流的速度，可根据甲在0至2小时走的路程-2至2.5小时的路程+2.5至3.5小时的路程=24千米，求出顺流的速度，然后根据不同的x的范围，用待定系数法求出y与x的函数关系式．

（4）根据（3）求出的顺流的速度可求出水流的速度，然后根据船追救生圈的距离+救生圈顺水的距离=二者在掉落时间到追及时间拉开的距离．求出自变量的值，进而求出甲船到A港的距离．

甲、乙两人（甲骑自行车，乙骑摩托车）从A城出发到B城旅行．如图表示甲、乙两人离开A城的路程与时间之间关系的图象．
（1）分别求出甲、乙两人这次旅程的平均速度是多少？
（2）根据图象，你能得出关于甲、乙两人旅行的哪些信息？
注：回答2时注意以下要求：
①请至少提供四条相关信息，如由图象可知，乙比甲早出发4小时（或甲比乙晚出发4小时）等；
②不要再提供（1）列举的信息．