
题目列表(包括答案和解析)
如图,已知⊙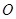 中,直径
中,直径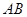 垂直于弦
垂直于弦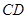 ,垂足为
,垂足为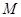 ,
,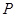 是
是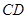 延长线上一点,
延长线上一点,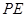 切⊙
切⊙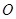 于点
于点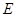 ,连接
,连接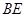 交
交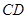 于点
于点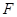 ,证明:
,证明: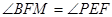
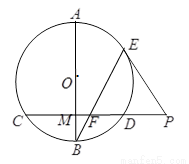
【解析】本试题主要考查了直线与圆的位置关系的运用。要证明角相等,一般运用相似三角形来得到,或者借助于弦切角定理等等。根据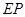 为⊙
为⊙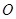 的切线,∴
的切线,∴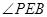 为弦切角
为弦切角
连接 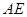 ∴
∴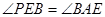 …注意到
…注意到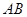 是直径且垂直弦
是直径且垂直弦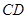 ,所以
,所以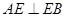 且
且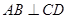 …利用
…利用 ,可以证明。
,可以证明。
解:∵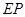 为⊙
为⊙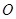 的切线,∴
的切线,∴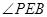 为弦切角
为弦切角
连接 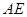 ∴
∴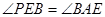 ……………………4分
……………………4分
又∵ 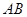 是直径且垂直弦
是直径且垂直弦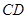 ∴
∴ 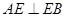 且
且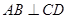 ……………………8分
……………………8分
∴  ∴
∴ 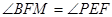
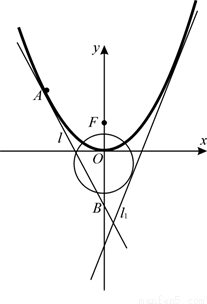
如图,已知直线 (
(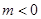 )与抛物线
)与抛物线 :
: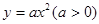 和圆
和圆 :
: 都相切,
都相切, 是
是 的焦点.
的焦点.
(Ⅰ)求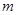 与
与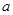 的值;
的值;
(Ⅱ)设 是
是 上的一动点,以
上的一动点,以 为切点作抛物线
为切点作抛物线 的切线
的切线 ,直线
,直线 交
交 轴于点
轴于点 ,以
,以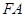 、
、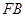 为邻边作平行四边形
为邻边作平行四边形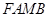 ,证明:点
,证明:点 在一条定直线上;
在一条定直线上;
(Ⅲ)在(Ⅱ)的条件下,记点 所在的定直线为
所在的定直线为 , 直线
, 直线 与
与 轴交点为
轴交点为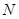 ,连接
,连接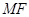 交抛物线
交抛物线 于
于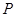 、
、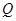 两点,求△
两点,求△ 的面积
的面积 的取值范围.
的取值范围.
【解析】第一问中利用圆 :
:
 的圆心为
的圆心为 ,半径
,半径 .由题设圆心到直线
.由题设圆心到直线 的距离
的距离 .
.
即 ,解得
,解得 (
( 舍去)
舍去)
设 与抛物线的相切点为
与抛物线的相切点为 ,又
,又 ,得
,得 ,
, .
.
代入直线方程得: ,∴
,∴ 所以
所以 ,
,
第二问中,由(Ⅰ)知抛物线 方程为
方程为 ,焦点
,焦点 . ………………(2分)
. ………………(2分)
设 ,由(Ⅰ)知以
,由(Ⅰ)知以 为切点的切线
为切点的切线 的方程为
的方程为 .
.
令 ,得切线
,得切线 交
交 轴的
轴的 点坐标为
点坐标为 所以
所以 ,
, , ∵四边形FAMB是以FA、FB为邻边作平行四边形
, ∵四边形FAMB是以FA、FB为邻边作平行四边形
∴ 因为
因为 是定点,所以点
是定点,所以点 在定直线
在定直线
第三问中,设直线 ,代入
,代入 得
得 结合韦达定理得到。
结合韦达定理得到。
解:(Ⅰ)由已知,圆 :
:
 的圆心为
的圆心为 ,半径
,半径 .由题设圆心到直线
.由题设圆心到直线 的距离
的距离 .
.
即 ,解得
,解得 (
( 舍去). …………………(2分)
舍去). …………………(2分)
设 与抛物线的相切点为
与抛物线的相切点为 ,又
,又 ,得
,得 ,
, .
.
代入直线方程得: ,∴
,∴ 所以
所以 ,
, .
……(2分)
.
……(2分)
(Ⅱ)由(Ⅰ)知抛物线 方程为
方程为 ,焦点
,焦点 . ………………(2分)
. ………………(2分)
设 ,由(Ⅰ)知以
,由(Ⅰ)知以 为切点的切线
为切点的切线 的方程为
的方程为 .
.
令 ,得切线
,得切线 交
交 轴的
轴的 点坐标为
点坐标为 所以
所以 ,
, , ∵四边形FAMB是以FA、FB为邻边作平行四边形,
, ∵四边形FAMB是以FA、FB为邻边作平行四边形,
∴ 因为
因为 是定点,所以点
是定点,所以点 在定直线
在定直线 上.…(2分)
上.…(2分)
(Ⅲ)设直线 ,代入
,代入 得
得 , ……)得
, ……)得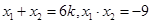 ,
…………………………… (2分)
,
…………………………… (2分)
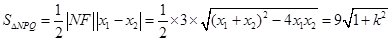 ,
,
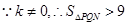 .
. △
△ 的面积
的面积 范围是
范围是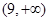
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com