
题目列表(包括答案和解析)
A.![]() B.
B.![]() C.
C.![]() D.不存在
D.不存在
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
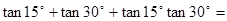 (
)
(
)
A.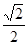 B.1 C.
B.1 C. D.
D.
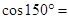 ( )
( )
A. B.
B.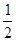 C.
C. D.
D.
一、选择题
CBACD ADBAC DB
二、填空题
13..files/image151.gif) 14.20 15.
14.20 15..files/image153.gif) 16.①③④
16.①③④
三、解答题
17.解:(1)由题设.files/image155.gif)
.files/image157.gif) ……………………2分
……………………2分
.files/image159.gif)
.files/image161.gif)
.files/image163.gif) …………………………3分
…………………………3分
由.files/image165.gif)
得.files/image167.gif) …………………………5分
…………………………5分
.files/image169.gif)
.files/image171.gif)
.files/image173.gif) …………………………6分
…………………………6分
(2)设.files/image112.gif) 图象向左平移m个单位,得到函数
图象向左平移m个单位,得到函数.files/image176.gif) 的图象.
的图象.
则.files/image178.gif) ,…………………………8分
,…………………………8分
.files/image180.gif) 对称,
对称,
.files/image182.gif) …………………………10分
…………………………10分
.files/image184.gif)
.files/image186.gif)
.files/image188.gif) …………………………12分
…………………………12分
18.(本小题满分12分)
解:(1)设等差数列.files/image072.gif) 的公差为d,等比数列的公比为q,
的公差为d,等比数列的公比为q,
由题设知.files/image191.gif)
.files/image193.gif)
则.files/image195.gif)
.files/image197.gif) ……………………3分
……………………3分
.files/image199.gif)
又.files/image201.gif)
又.files/image203.gif)
.files/image205.gif)
.files/image207.gif) ,
,
.files/image209.gif) …………………………6分
…………………………6分
(2).files/image211.gif) …………………………7分
…………………………7分
.files/image213.gif)
.files/image215.gif) ①
①
.files/image217.gif) ②……………………9分
②……………………9分
①―②得.files/image219.gif)
.files/image221.gif)
.files/image223.gif) …………………………12分
…………………………12分
19.(本小题满分12分)
证明:(1)取AC中点O,
|