22. （本小题满分12分）

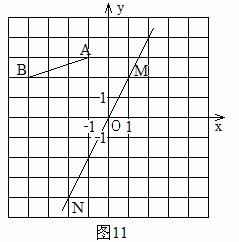
如图11，在方格纸上建立平面直角坐标系，线段AB的两个端点都在格点上，直线MN经过坐标原点，且点M的坐标是（1，2）。

（1）写出点A、B的坐标；

（2）求直线MN所对应的函数关系式；

（3）利用尺规作出线段AB关于直线MN的对称图形（保留作图痕迹，不写作法）。

（11·大连）（本题12分）如图7，某建筑物BC上有一旗杆AB，小明在与BC

相距12m的F处，由E点观测到旗杆顶部A的仰角为52°、底部B的仰角为45°，小明的

观测点与地面的距离EF为1.6m．

⑴求建筑物BC的高度；

⑵求旗杆AB的高度．

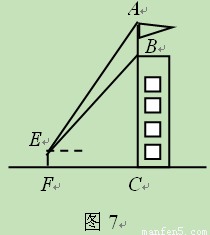
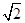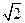（结果精确到0.1m．参考数据：≈1.41，sin52°≈0.79，tan52°≈1.28）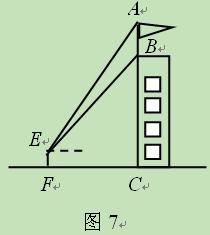

 

（11·大连）（本题12分）如图7，某建筑物BC上有一旗杆AB，小明在与BC
相距12m的F处，由E点观测到旗杆顶部A的仰角为52°、底部B的仰角为45°，小明的
观测点与地面的距离EF为1.6m．
⑴求建筑物BC的高度；
⑵求旗杆AB的高度．
（结果精确到0.1m．参考数据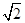：≈1.41，sin52°≈0.79，tan52°≈1.28）

（11·十堰）12分）如图，已知抛物线y=x2+bx+c与x轴交于点A（1，0）和点B，与y轴交于点C（0，-3）。
（1）求抛物线的解析式；
（2）如图（1），已知点H（0，-1）.问在抛物线上是否存在点G（点G在y轴的左侧），使得S_△GHC=S_△GHA？若存在，求出点G的坐标，若不存在，请说明理由；
（3）如图（2），抛物线上点D在x轴上的正投影为点E（-2，0），F是OC的中点，连接DF，P为线段BD上的一点，若∠EPF=∠BDF，求线段PE的长.

（11·大连）（本题12分）如图7，某建筑物BC上有一旗杆AB，小明在与BC

相距12m的F处，由E点观测到旗杆顶部A的仰角为52°、底部B的仰角为45°，小明的

观测点与地面的距离EF为1.6m．

⑴求建筑物BC的高度；

⑵求旗杆AB的高度．

（结果精确到0.1m．参考数据：≈1.41，sin52°≈0.79，tan52°≈1.28）