
题目列表(包括答案和解析)
(本小题满分12分)二次函数![]() 的图象经过三点
的图象经过三点![]() .
.![]()
(1)求函数![]() 的解析式(2)求函数
的解析式(2)求函数![]() 在区间
在区间![]() 上的最大值和最小值
上的最大值和最小值
(本小题满分12分)已知等比数列{an}中,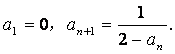
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)设数列{an}的前n项和为Sn,证明:![]() ;
;
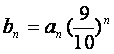 ,证明:对任意的正整数n、m,均有
,证明:对任意的正整数n、m,均有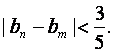
(本小题满分12分)已知函数![]() ,其中a为常数.
,其中a为常数.
(Ⅰ)若当![]() 恒成立,求a的取值范围;
恒成立,求a的取值范围;
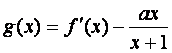 的单调区间.
的单调区间.(本小题满分12分)
甲、乙两篮球运动员进行定点投篮,每人各投4个球,甲投篮命中的概率为![]() ,乙投篮命中的概率为
,乙投篮命中的概率为![]()
(Ⅰ)求甲至多命中2个且乙至少命中2个的概率;
(Ⅱ)若规定每投篮一次命中得3分,未命中得-1分,求乙所得分数η的概率分布和数学期望.(本小题满分12分)已知![]() 是椭圆
是椭圆![]() 的两个焦点,O为坐标原点,点
的两个焦点,O为坐标原点,点![]() 在椭圆上,且
在椭圆上,且![]() ,圆O是以
,圆O是以![]() 为直径的圆,直线
为直径的圆,直线![]() 与圆O相切,并且与椭圆交于不同的两点A、B.
与圆O相切,并且与椭圆交于不同的两点A、B.
(1)求椭圆的标准方程;w.w.w.k.s.5.u.c.o.m ![]()
![]()
(2)当![]() 时,求弦长|AB|的取值范围.
时,求弦长|AB|的取值范围.
一.选择题
1.B 2.B 3. A 4.A 5.C 6. D 7.B 8.D 9.B 10.A 11.C 12.C
二.填空题
13.(1, 文数.files/image188.gif) )∪(
)∪(文数.files/image188.gif) ,2)
14.
,2)
14.文数.files/image190.gif) 15.
15.文数.files/image192.gif) 16. ②③④
16. ②③④
三.解答题
文数.files/image193.gif) 17.解:(1)两学生成绩绩的茎叶图如图所示……………4分
17.解:(1)两学生成绩绩的茎叶图如图所示……………4分
(2)将甲、乙两学生的成绩从小到大排列为:
甲: 512 522 528 534 536 538 541 549 554 556
乙:515 521 527 531 532 536 543 548 558 559
从以上排列可知甲学生成绩的中位数为文数.files/image195.gif) ……6分
……6分
乙学生成绩的中位数为文数.files/image197.gif) …………8分
…………8分
甲学生成绩的平均数为:
文数.files/image199.gif) ……………10分
……………10分
乙学生成绩的平均数为:
文数.files/image201.gif) ……………12分
……………12分
18.解:(1)∵文数.files/image203.gif)
∴文数.files/image205.gif) ,
,
∴文数.files/image207.gif) ,∴
,∴文数.files/image209.gif) ∵
∵ 文数.files/image211.gif) ∈(0,π)
∴
∈(0,π)
∴文数.files/image213.gif) ……4分
……4分
(2)∵文数.files/image215.gif) ∴
∴文数.files/image217.gif) ,即
,即文数.files/image219.gif) ① …………6分
① …………6分
又文数.files/image221.gif) ∴
∴文数.files/image223.gif) ,即
,即文数.files/image225.gif) ② …………8分
② …………8分
由①②可得文数.files/image227.gif) ,∴
,∴文数.files/image229.gif) ………………………………………10分
………………………………………10分
又文数.files/image231.gif) ∴
∴文数.files/image233.gif) , ……………………………………12分
, ……………………………………12分
高三数学试题答案(文科)(共4页)第1页
19.(I)设文数.files/image235.gif) 是
是文数.files/image237.gif) 的中点,连结
的中点,连结文数.files/image239.gif) ,则四边形
,则四边形文数.files/image241.gif) 为正方形,……………2分
为正方形,……………2分
文数.files/image243.gif) .故
.故文数.files/image245.gif) ,
,文数.files/image247.gif) ,
,文数.files/image249.gif) ,
,文数.files/image251.gif) ,即
,即文数.files/image253.gif) .
.
………………………4分
又文数.files/image255.gif) ,
,文数.files/image257.gif)
文数.files/image259.gif) 平面
平面文数.files/image261.gif) ,…………………………6分
,…………………………6分
(II)证明:DC的中点即为E点, ………………………………………………8分
连D1E,BE文数.files/image263.gif)
文数.files/image265.gif) ∴四边形ABED是平行四边形,
∴四边形ABED是平行四边形,
∴AD文数.files/image267.gif) BE,又AD
BE,又AD文数.files/image267.gif) A1D1
A1D1 文数.files/image270.gif)
文数.files/image267.gif) A1D1 ∴四边形A1D1EB是平行四边形
A1D1 ∴四边形A1D1EB是平行四边形 文数.files/image272.gif) D1E//A1B ,
D1E//A1B ,
∵D1E文数.files/image274.gif) 平面A1BD ∴D1E//平面A1BD。……………………………………………12分
平面A1BD ∴D1E//平面A1BD。……………………………………………12分
20.解:(1)设这二次函数f(x)=ax2+bx (a≠0) ,则文数.files/image276.gif)
得a=3 , b=-2, 所以 f(x)=3x2-2x. ……………………………………3分
又因为点文数.files/image278.gif) 均在函数
均在函数文数.files/image280.gif) 的图像上,所以
的图像上,所以文数.files/image282.gif) =3n2-2n.
=3n2-2n.
当n≥2时,an=Sn-Sn-1=(3n2-2n)-文数.files/image284.gif) =6n-5.
=6n-5.
当n=1时,a1=S1=3×12-2=6×1-5,所以,an=6n-5 (文数.files/image286.gif) )………6分
)………6分
(2)由(1)得知文数.files/image288.gif) =
=文数.files/image290.gif) =
=文数.files/image292.gif) ,……8分
,……8分
故Tn=文数.files/image294.gif) =
=文数.files/image296.gif)
文数.files/image298.gif) =
=文数.files/image296.gif) (1-
(1-文数.files/image300.gif) )………10分
)………10分
因此,要使文数.files/image296.gif) (1-
(1-文数.files/image301.gif) )<
)<文数.files/image303.gif) (
(文数.files/image286.gif) )成立的m,必须且仅须满足
)成立的m,必须且仅须满足
文数.files/image296.gif) ≤
≤文数.files/image303.gif) ,即m≥10,所以满足要求的最小正整数m为10. ………………………12分
,即m≥10,所以满足要求的最小正整数m为10. ………………………12分
|