
题目列表(包括答案和解析)
已知直线 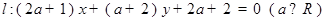 ,有下列四个结论:
,有下列四个结论:
① 若 =
= ,则直线
,则直线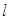 与
与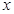 轴平行
; ②若
轴平行
; ②若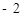 <
< <
<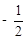 ,则直线
,则直线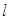 单调递增;
单调递增;
③当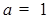 时,
时,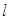 与两坐标轴围成的三角形面积为
与两坐标轴围成的三角形面积为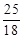 ; ④
; ④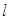 经过定点
经过定点
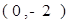 ;
;
⑤ 当 ∈ [ 1, 4+3
∈ [ 1, 4+3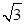 ]
时,直线l的倾斜角
]
时,直线l的倾斜角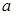 满足
满足
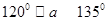 ;
;
其中正确结论的是 (填上你认为正确的所有序号).
已知直线![]() 经过两点
经过两点![]() ,问:当
,问:当![]() 取何值时
取何值时
(1)直线![]() 与
与![]() 轴平行? (2)
轴平行? (2)![]() 与
与![]() 轴平行? (3)
轴平行? (3)![]() 的斜率为
的斜率为![]() 。
。
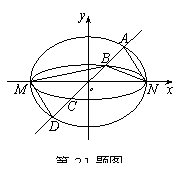
如图,已知椭圆![]() 与
与![]() 的中心在坐标原点
的中心在坐标原点![]() ,长轴均为
,长轴均为![]() 且在
且在![]() 轴上,短轴长分别为
轴上,短轴长分别为![]() ,
,![]()
![]() ,过原点且不与
,过原点且不与![]() 轴重合的直线
轴重合的直线![]() 与
与![]() ,
,![]() 的四个交点按纵坐标从大到小依次为
的四个交点按纵坐标从大到小依次为![]() ,
,![]() ,
,![]() ,
,![]() 。记
。记![]() ,
,![]() 和
和![]() 的面积分别为
的面积分别为![]() 和
和![]() 。
。
(I)当直线![]() 与
与![]() 轴重合时,若
轴重合时,若![]() ,求
,求![]() 的值;
的值;
(II)当![]() 变化时,是否存在与坐标轴不重合的直线
变化时,是否存在与坐标轴不重合的直线![]() ,使得
,使得![]() ?并说明理由。
?并说明理由。
已知焦点在![]() 轴上的椭圆C1:
轴上的椭圆C1:![]() =1经过A(1,0)点,且离心率为
=1经过A(1,0)点,且离心率为![]() .
.
(I)求椭圆C1的方程;
(Ⅱ)过抛物线C2:![]() (h∈R)上P点的切线与椭圆C1交于两点M、N,记线段MN与PA的中点分别为G、H,当GH与
(h∈R)上P点的切线与椭圆C1交于两点M、N,记线段MN与PA的中点分别为G、H,当GH与![]() 轴平行时,求h的最小值.
轴平行时,求h的最小值.
已知焦点在![]() 轴上的椭圆C1:
轴上的椭圆C1:![]() =1经过A(1,0)点,且离心率为
=1经过A(1,0)点,且离心率为![]() .(1)求椭圆C1的方程;
.(1)求椭圆C1的方程;
(2)过抛物线C2:![]() (h∈R)上P点的切线与椭圆C1交于两点M、N,记线段MN与PA的中点分别为G、H,当GH与
(h∈R)上P点的切线与椭圆C1交于两点M、N,记线段MN与PA的中点分别为G、H,当GH与![]() 轴平行时,求h的最小值.
轴平行时,求h的最小值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com