
题目列表(包括答案和解析)
| C | m n |
| n |
| m |
| C | m-1 n-1 |
| (1+x)[1-(1+x)n] |
| 1-(1+x) |
| (1+x)n+1-(1+x) |
| x |
()某企业有3个分厂生产同一种电子产品,第一、二、三分厂的产量之比为1:2:1,用分层抽样方法(每个分厂的产品为一层)从3个分厂生产的电子产品中共取100件作使用寿命的测试,由所得的测试结果算得从第一、二、三分厂取出的产品的使用寿命的平均值分别为980h,1020h,1032h,则抽取的100件产品的使用寿命的平均值为 h.
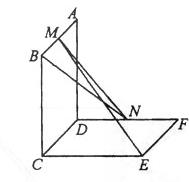
()如图,已知两个正方行ABCD 和DCEF不在同一平面内,M,N分别为AB,DF的中点 。
(I)若平面ABCD ⊥平面DCEF,求直线MN与平面DCEF所成角的正值弦;
(II)用反证法证明:直线ME 与 BN 是两条异面直线。![]()
![]()
()某工厂有工人1000名, 其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人),现用分层抽样方法(按A类、B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数)。
(I)求甲、乙两工人都被抽到的概率,其中甲为A类工人,乙为B类工人;
(II)从A类工人中的抽查结果和从B类工人中的抽插结果分别如下表1和表2.
表1:
| 生产能力分组 |
|
|
|
|
|
| 人数 | 4 | 8 |
| 5 | 3 |
表2:
| 生产能力分组 |
|
|
|
|
| 人数 | 6 | y | 36 | 18 |
(i)先确定x,y,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
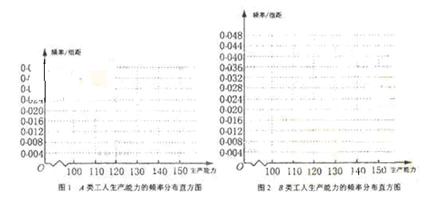
(ii)分别估计A类工人和B类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数,同一组中的数据用该组区间的中点值作代表)
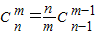 ;
;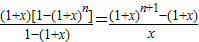 ;,由左边可求得x2的系数为C22+C32+C42+…+Cn2,利用右式可得x2的系数为Cn+13,所以C22+C32+C42+…+Cn2=Cn+13.请利用此方法证明:(C2n)2-(C2n1)2+(C2n2)2-(C2n3)2+…+(C2n2n)2=(-1)nC2nn.
;,由左边可求得x2的系数为C22+C32+C42+…+Cn2,利用右式可得x2的系数为Cn+13,所以C22+C32+C42+…+Cn2=Cn+13.请利用此方法证明:(C2n)2-(C2n1)2+(C2n2)2-(C2n3)2+…+(C2n2n)2=(-1)nC2nn.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com