
题目列表(包括答案和解析)
已知函数 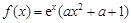
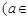 R).
R).
(Ⅰ)若  ,求曲线
,求曲线
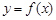 在点
在点 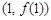 处的的切线方程;
处的的切线方程;
(Ⅱ)若 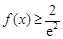 对任意
对任意 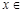
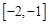 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【解析】本试题主要考查了导数在研究函数中的运用。
第一问中,利用当 时,
时,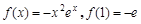 .
.
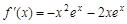 因为切点为(
因为切点为(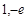 ),
则
),
则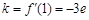 ,
,
所以在点(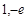 )处的曲线的切线方程为:
)处的曲线的切线方程为:
第二问中,由题意得, 即
即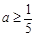 即可。
即可。
Ⅰ)当 时,
时,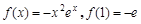 .
.
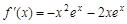 ,
,
因为切点为(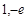 ),
则
),
则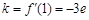 ,
,
所以在点(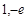 )处的曲线的切线方程为:
)处的曲线的切线方程为: . ……5分
. ……5分
(Ⅱ)解法一:由题意得, 即
即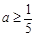 . ……9分
. ……9分
(注:凡代入特殊值缩小范围的均给4分)
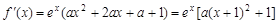 ,
,
因为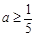 ,所以
,所以 恒成立,
恒成立,
故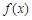 在
在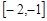 上单调递增,
……12分
上单调递增,
……12分
要使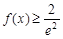 恒成立,则
恒成立,则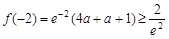 ,解得
,解得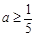 .……15分
.……15分
解法二: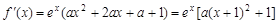 ……7分
……7分
(1)当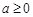 时,
时, 在
在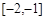 上恒成立,
上恒成立,
故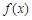 在
在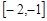 上单调递增,
上单调递增,
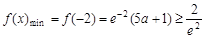 即
即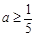 .
……10分
.
……10分
(2)当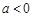 时,令
时,令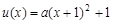 ,对称轴
,对称轴 ,
,
则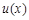 在
在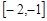 上单调递增,又
上单调递增,又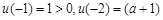
① 当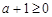 ,即
,即 时,
时,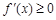 在
在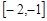 上恒成立,
上恒成立,
所以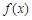 在
在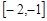 单调递增,
单调递增,
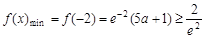 即
即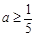 ,不合题意,舍去
,不合题意,舍去
②当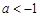 时,
时,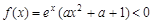 ,
不合题意,舍去 14分
,
不合题意,舍去 14分
综上所述: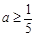
(本题满分12分)探究函数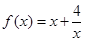 ,
,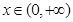 的最小值,并确定取得最小值时
的最小值,并确定取得最小值时 的值,列表如下:
的值,列表如下:
|
|
… |
0.5 |
1 |
1.5 |
1.7 |
1.9 |
2 |
2.1 |
2.2 |
2.3 |
3 |
4 |
5 |
7 |
… |
|
|
… |
8.5 |
5 |
4.17 |
4.05 |
4.005 |
4 |
4.005 |
4.102 |
4.24 |
4.3 |
5 |
5.8 |
7.57 |
… |
请观察表中 值随
值随 值变化的特点,完成下列问题:
值变化的特点,完成下列问题:
(1) 当 时,
时,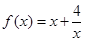 在区间
在区间 上递减,在区间 上递增;
上递减,在区间 上递增;
所以, =
时,
=
时,  取到最小值为
;
取到最小值为
;
(2) 由此可推断,当 时,
时,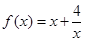 有最
值为 ,此时
有最
值为 ,此时 =
;
=
;
(3) 证明: 函数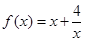 在区间
在区间 上递减;
上递减;
(4) 若方程 在
在 内有两个不相等的实数根,求实数
内有两个不相等的实数根,求实数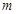 的取值范围。
的取值范围。
(本题满分12分)探究函数![]() ,
,![]() 的最小值,并确定取得最小值时
的最小值,并确定取得最小值时![]() 的值,列表如下:
的值,列表如下:
|
| … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
|
| … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.102 | 4.24 | 4.3 | 5 | 5.8 | 7.57 | … |
请观察表中![]() 值随
值随![]() 值变化的特点,完成下列问题:
值变化的特点,完成下列问题:
(1) 当![]() 时,
时,![]() 在区间
在区间![]() 上递减,在区间 上递增;
上递减,在区间 上递增;
所以,![]() = 时,
= 时, ![]() 取到最小值为 ;
取到最小值为 ;
(2) 由此可推断,当![]() 时,
时,![]() 有最 值为 ,此时
有最 值为 ,此时![]() = ;
= ;
(3) 证明: 函数![]() 在区间
在区间![]() 上递减;
上递减;
(4) 若方程![]() 在
在![]() 内有两个不相等的实数根,求实数
内有两个不相等的实数根,求实数![]() 的取值范围。
的取值范围。
设函数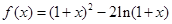 .
.
(I)求 的单调区间;
的单调区间;
(II)当0<a<2时,求函数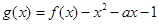 在区间
在区间 上的最小值.
上的最小值.
【解析】第一问定义域为真数大于零,得到 .
. .
.
令 ,则
,则 ,所以
,所以 或
或 ,得到结论。
,得到结论。
第二问中, (
( ).
).
 .
.
因为0<a<2,所以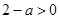 ,
, .令
.令 可得
可得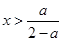 .
.
对参数讨论的得到最值。
所以函数 在
在 上为减函数,在
上为减函数,在 上为增函数.
上为增函数.
(I)定义域为 . ………………………1分
. ………………………1分
 .
.
令 ,则
,则 ,所以
,所以 或
或 . ……………………3分
. ……………………3分
因为定义域为 ,所以
,所以 .
.
令 ,则
,则 ,所以
,所以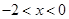 .
.
因为定义域为 ,所以
,所以 . ………………………5分
. ………………………5分
所以函数的单调递增区间为 ,
,
单调递减区间为 .
………………………7分
.
………………………7分
(II) (
( ).
).
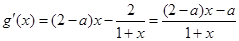 .
.
因为0<a<2,所以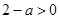 ,
, .令
.令 可得
可得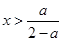 .…………9分
.…………9分
所以函数 在
在 上为减函数,在
上为减函数,在 上为增函数.
上为增函数.
①当 ,即
,即 时,
时,
在区间 上,
上, 在
在 上为减函数,在
上为减函数,在 上为增函数.
上为增函数.
所以 . ………………………10分
. ………………………10分
②当 ,即
,即 时,
时, 在区间
在区间 上为减函数.
上为减函数.
所以 .
.
综上所述,当 时,
时, ;
;
当 时,
时,
(本题满分12分)
某桶装水经营部每天的房租,人员工资等固定成本为200元,每桶水的进价是5元。销售单价与日均销售的关系如下表所示
|
销售单价(元) |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
日均销售量(桶) |
480 |
440 |
400 |
360 |
320 |
280 |
240 |
设在进价基础上增加x元后,日均销售利润为y元。
(1)写出日均销售量P与x的函数关系式,标出定义域;
(2)请根据以上数据作出分析:这个经营部怎样定价才能获得最大利润?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com