
题目列表(包括答案和解析)
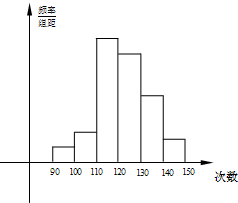 为了解高一学生的体能状况,某校抽取部分学生(样本容量为n)进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形的高之比为2:4:17:15:9:3,第二小组频数为12.
为了解高一学生的体能状况,某校抽取部分学生(样本容量为n)进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形的高之比为2:4:17:15:9:3,第二小组频数为12.| 分组 | 频数 | 频率 |
| [90,100) | ||
| [100,110) | 12 | |
| [110,120) | ||
| [120,130) | ||
| [130,140) | ||
| [140,150) | ||
| 合计 | 1 |
已知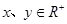 ,且
,且 ,求
,求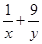 的最小值.某同学做如下解答:
的最小值.某同学做如下解答:
因为 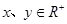 ,所以
,所以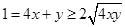 ┄①,
┄①, ┄②,
┄②,
①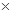 ②得
②得  ,所以
,所以
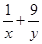 的最小值为24.
的最小值为24.
判断该同学解答是否正确,若不正确,请在以下空格内填写正确的最小值;若正确,请在以下空格内填写取得最小值时 、
、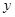 的值. .
的值. .
已知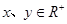 ,且
,且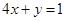 ,求
,求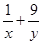 的最小值.某同学做如下解答:
的最小值.某同学做如下解答:
因为 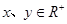 ,所以
,所以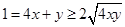 ┄①,
┄①,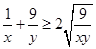 ┄②,
┄②,
①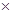 ②得
②得 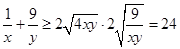 ,所以
,所以
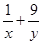 的最小值为24.
的最小值为24.
判断该同学解答是否正确,若不正确,请在以下空格内填写正确的最小值;若正确,请在以下空格内填写取得最小值时 、
、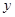 的值. .
的值. .
给出以下4个命题:
①曲线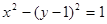 按
按 平移可得曲线
平移可得曲线 ;
;
②若| -1|+|
-1|+|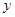 -1|
-1| ,则使
,则使

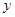 取得最小值的最优解有无数多个;
取得最小值的最优解有无数多个;
③设 、
、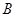 为两个定点,
为两个定点,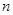 为常数,
为常数,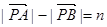 ,则动点
,则动点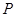 的轨迹为双曲线;
的轨迹为双曲线;
④若椭圆的左、右焦点分别为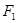 、
、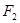 ,
,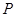 是该椭圆上的任意一点,延长
是该椭圆上的任意一点,延长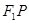 到点
到点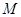 ,使
,使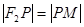 ,则点
,则点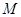 的轨迹是圆.
的轨迹是圆.
其中所有真命题的序号为 .
已知 ,且
,且 ,求
,求 的最小值.某同学做如下解答:
的最小值.某同学做如下解答:
因为  ,所以
,所以 ┄①,
┄①, ┄②,
┄②,
① ②得
②得  ,所以
,所以  的最小值为24.
的最小值为24.
判断该同学解答是否正确,若不正确,请在以下空格内填写正确的最小值;若正确,请在以下空格内填写取得最小值时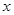 、
、 的值. .
的值. .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com