
题目列表(包括答案和解析)
设数列 的各项均为正数.若对任意的
的各项均为正数.若对任意的 ,存在
,存在 ,使得
,使得 成立,则称数列
成立,则称数列 为“Jk型”数列.
为“Jk型”数列.
(1)若数列 是“J2型”数列,且
是“J2型”数列,且 ,
, ,求
,求 ;
;
(2)若数列 既是“J3型”数列,又是“J4型”数列,证明:数列
既是“J3型”数列,又是“J4型”数列,证明:数列 是等比数列.
是等比数列.
【解析】1)中由题意,得 ,
, ,
, ,
, ,…成等比数列,且公比
,…成等比数列,且公比 ,
,
所以.
(2)中证明:由{ }是“j4型”数列,得
}是“j4型”数列,得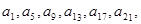 ,…成等比数列,设公比为t. 由{
,…成等比数列,设公比为t. 由{ }是“j3型”数列,得
}是“j3型”数列,得
 ,…成等比数列,设公比为
,…成等比数列,设公比为 ;
;
 ,…成等比数列,设公比为
,…成等比数列,设公比为 ;
;
 …成等比数列,设公比为
…成等比数列,设公比为 ;
;
(本题满分12分)
为考察某种甲型H1N1疫苗的效果,进行动物实验,得到如下疫苗效果的实验列联表:
|
|
感染 |
未感染 |
总计 |
|
没服用 |
20 |
30 |
50 |
|
服用 |
x |
y |
50 |
|
总计 |
M |
N |
100 |
设从没服用疫苗的动物中任取两只,感染数为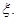 从服从过疫苗的动物中任取两只,感染数为
从服从过疫苗的动物中任取两只,感染数为 工作人员曾计算过
工作人员曾计算过
(1)求出列联表中数据 的值;
的值;
(2)写出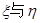 的均值(不要求计算过程),并比较大小,请解释所得出的结论的实际意义;
的均值(不要求计算过程),并比较大小,请解释所得出的结论的实际意义;
(3)能够以97.5%的把握认为这种甲型H1N1疫苗有效么?并说明理由。
参考公式:
参考数据:
|
|
0.05 |
0.025 |
0.010 |
|
|
3.841 |
5.024 |
6.635 |
(本题满分12分)
为考察某种甲型H1N1疫苗的效果,进行动物实验,得到如下疫苗效果的实验列联表:
| | 感染 |  未感染 未感染 | 总计 |
| 没服用 | 20 | 30 | 50 |
| 服用 | x | y | 50 |
| 总计 | M | N | 100 |
 从服从过疫苗的动物中任取两只,感染数为
从服从过疫苗的动物中任取两只,感染数为 工作人员曾计算过
工作人员曾计算过
 (
( 1)求出列联表中数据
1)求出列联表中数据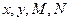 的值;
的值; 的均值(不要求计算过程),并比较大小,请解释所得出的结论的实际意义;
的均值(不要求计算过程),并比较大小,请解释所得出的结论的实际意义;
 参考数据:
参考数据: | 0.05 | 0.025 | 0.010 |
 | 3.841 | 5.024 | 6.635 |
| | 感染 |  未感染 未感染 | 总计 |
| 没服用 | 20 | 30 | 50 |
| 服用 | x | y | 50 |
| 总计 | M | N | 100 |
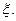 从服从过疫苗的动物中任取两只,感染数为
从服从过疫苗的动物中任取两只,感染数为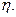 工作人员曾计算过
工作人员曾计算过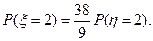
 (
( 1)求出列联表中数据
1)求出列联表中数据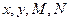 的值;
的值;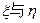 的均值(不要求计算过程),并比较大小,请解释所得出的结论的实际意义;
的均值(不要求计算过程),并比较大小,请解释所得出的结论的实际意义;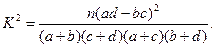
 参考数据:
参考数据: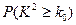 | 0.05 | 0.025 | 0.010 |
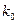 | 3.841 | 5.024 | 6.635 |
设数列{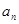 }的前n项和
}的前n项和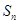 满足:
满足: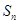 =n
=n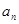 -2n(n-1).等比数列{
-2n(n-1).等比数列{ }的前n项和为
}的前n项和为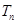 ,公比为
,公比为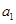 ,且
,且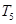 =
=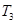 +2
+2 .
.
(1)求数列{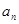 }的通项公式;
}的通项公式;
(2)设数列{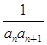 }的前n项和为
}的前n项和为 ,求证:
,求证: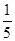 ≤
≤ <
<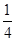 .
.
【解析】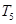 =
=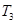 +2
+2 求出
求出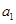 ,由
,由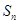 =n
=n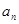 -2n(n-1)递写一个式子相减,得{
-2n(n-1)递写一个式子相减,得{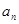 }为等差数列;(2)裂项法求
}为等差数列;(2)裂项法求 ,然后证明
,然后证明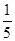 ≤
≤ <
<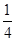 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com