
题目列表(包括答案和解析)
(1)已知: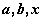 均是正数,且
均是正数,且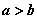 ,求证:
,求证: ;
;
(2)当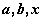 均是正数,且
均是正数,且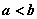 ,对真分数
,对真分数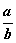 ,给出类似上小题的结论,并予以证明;
,给出类似上小题的结论,并予以证明;
(3)证明:△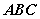 中,
中,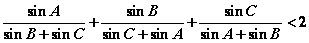 (可直接应用第(1)、(2)小题结论)
(可直接应用第(1)、(2)小题结论)
(4)自己设计一道可直接应用第(1)、(2)小题结论的不等式证明题,并写出证明过程.
| 1 |
| 2 |
| 2an2+an |
| an+1 |
| 2n |
 |
| i=1 |
| Sn |
| n2 |
已知函数f(x)的定义域为R,对任意实数m、n,均有f(m+n)=f(m)+f(n)-1,且f(-![]() )=0,当x>-
)=0,当x>-![]() 时,有
时,有
f(x)>0.
(1)求证:f(x)是单调递增函数;
(2)解不等式1+f(![]() )≤f(1)+f(ax),其中a为正常数.
)≤f(1)+f(ax),其中a为正常数.
 时,求数列{bn}的通项公式;
时,求数列{bn}的通项公式; ,Sn=
,Sn=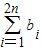 ,求证:2<
,求证:2<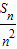 <6.
<6.(1)已知:a,b,x均是正数,且a>b,求证:![]() ;
;
(2)当a,b,x均是正数,且a<b,对真分数![]() ,给出类似上小题的结论,并予以证明;
,给出类似上小题的结论,并予以证明;
(3)证明:△ABC中,![]() (可直接应用第(1)、(2)小题结论)
(可直接应用第(1)、(2)小题结论)
(4)自己设计一道可直接应用第(1)、(2)小题结论的不等式证明题,并写出证明过程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com