
题目列表(包括答案和解析)
(本小题满分12分)
已知函数f(x)=lg(ax-bx)(a>1>b>0).
(1)求y=f(x)的定义域;
(2)在函数y=f(x)的图象上是否存在不同的两点,使得过这两点的直线平行于x轴;
(3)当a,b满足什么条件时,f(x)在(1,+∞)上恒取正值.
.(本小题满分12分)
已知函数f(x)=lg(ax-bx)(a>1>b>0).
(1)求y=f(x)的定义域;
(2)在函数y=f(x)的图象上是否存在不同的两点,使得过这两点的直线平行于x轴;
(3)当a,b满足什么条件时,f(x)在(1,+∞)上恒取正值.
(本小题满分12分)已知:y = f (x) 定义域为[–1,1],且满足:f (–1) = f (1) = 0 ,对任意u ,v??[–1,1],都有|f (u) – f (v) | ≤ | u –v | .(1) 判断函数p ( x ) = x2 – 1 是否满足题设条件?(2) 判断函数g(x)=![]() ,是否满足题设条件?
,是否满足题设条件?
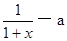 ,(f/(x))是f(x)的导数)
,(f/(x))是f(x)的导数)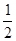
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com