
题目列表(包括答案和解析)
已知函数 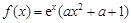
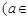 R).
R).
(Ⅰ)若  ,求曲线
,求曲线
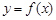 在点
在点 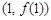 处的的切线方程;
处的的切线方程;
(Ⅱ)若 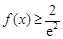 对任意
对任意 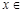
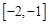 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【解析】本试题主要考查了导数在研究函数中的运用。
第一问中,利用当 时,
时,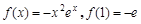 .
.
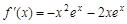 因为切点为(
因为切点为(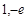 ),
则
),
则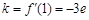 ,
,
所以在点(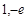 )处的曲线的切线方程为:
)处的曲线的切线方程为:
第二问中,由题意得, 即
即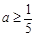 即可。
即可。
Ⅰ)当 时,
时,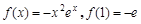 .
.
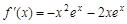 ,
,
因为切点为(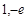 ),
则
),
则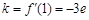 ,
,
所以在点(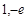 )处的曲线的切线方程为:
)处的曲线的切线方程为: . ……5分
. ……5分
(Ⅱ)解法一:由题意得, 即
即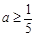 . ……9分
. ……9分
(注:凡代入特殊值缩小范围的均给4分)
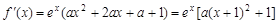 ,
,
因为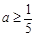 ,所以
,所以 恒成立,
恒成立,
故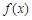 在
在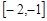 上单调递增,
……12分
上单调递增,
……12分
要使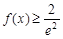 恒成立,则
恒成立,则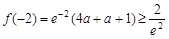 ,解得
,解得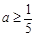 .……15分
.……15分
解法二: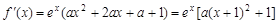 ……7分
……7分
(1)当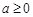 时,
时, 在
在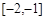 上恒成立,
上恒成立,
故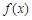 在
在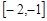 上单调递增,
上单调递增,
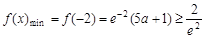 即
即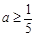 .
……10分
.
……10分
(2)当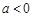 时,令
时,令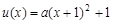 ,对称轴
,对称轴 ,
,
则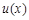 在
在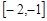 上单调递增,又
上单调递增,又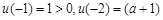
① 当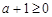 ,即
,即 时,
时,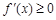 在
在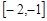 上恒成立,
上恒成立,
所以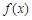 在
在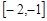 单调递增,
单调递增,
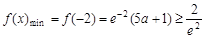 即
即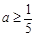 ,不合题意,舍去
,不合题意,舍去
②当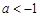 时,
时,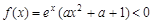 ,
不合题意,舍去 14分
,
不合题意,舍去 14分
综上所述: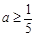
平面内与两定点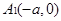 、
、
 连线的斜率之积等于非零常数
连线的斜率之积等于非零常数 的点的轨迹,加上
的点的轨迹,加上 、
、 两点所成的曲线
两点所成的曲线 可以是圆、椭圆或双曲线。求曲线
可以是圆、椭圆或双曲线。求曲线 的方程,并讨论
的方程,并讨论 的形状与
的形状与 值的关系。
值的关系。
【解析】本试题主要考查了平面中动点的轨迹方程,利用斜率之积为定值可以对参数进行分类讨论,并得到关于不同曲线的参数的范围问题。对于方程的特点做了很好的考查和运用。
平面内与两定点 、
、
 连线的斜率之积等于非零常数
连线的斜率之积等于非零常数 的点的轨迹,加上
的点的轨迹,加上 、
、 两点所成的曲线
两点所成的曲线 可以是圆、椭圆或双曲线。求曲线
可以是圆、椭圆或双曲线。求曲线 的方程,并讨论
的方程,并讨论 的形状与
的形状与 值的关系。
值的关系。
【解析】本试题主要考查了平面中动点的轨迹方程,利用斜率之积为定值可以对参数进行分类讨论,并得到关于不同曲线的参数的范围问题。对于方程的特点做了很好的考查和运用。
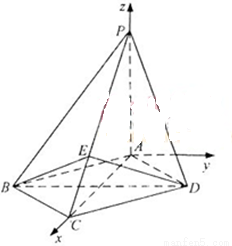
如图,四棱锥P-ABCD中,底面ABCD为菱形,PA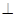 底面ABCD,AC=
底面ABCD,AC=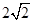 ,PA=2,E是PC上的一点,PE=2EC。
,PA=2,E是PC上的一点,PE=2EC。
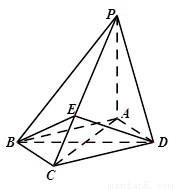
(I)
证明PC 平面BED;
平面BED;
(II) 设二面角A-PB-C为90°,求PD与平面PBC所成角的大小
【解析】本试题主要是考查了四棱锥中关于线面垂直的证明以及线面角的求解的运用。
从题中的线面垂直以及边长和特殊的菱形入手得到相应的垂直关系和长度,并加以证明和求解。
解法一:因为底面ABCD为菱形,所以BD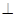 AC,又
AC,又
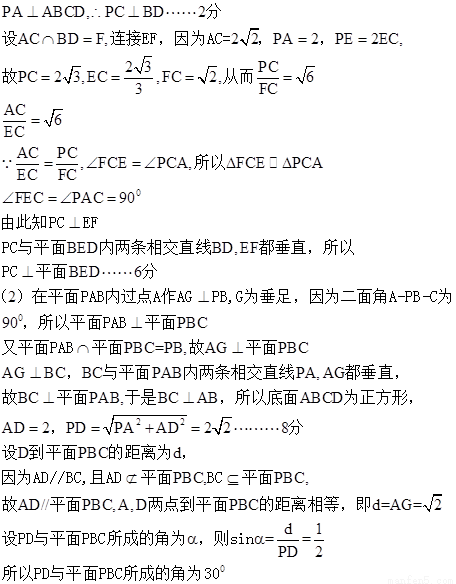

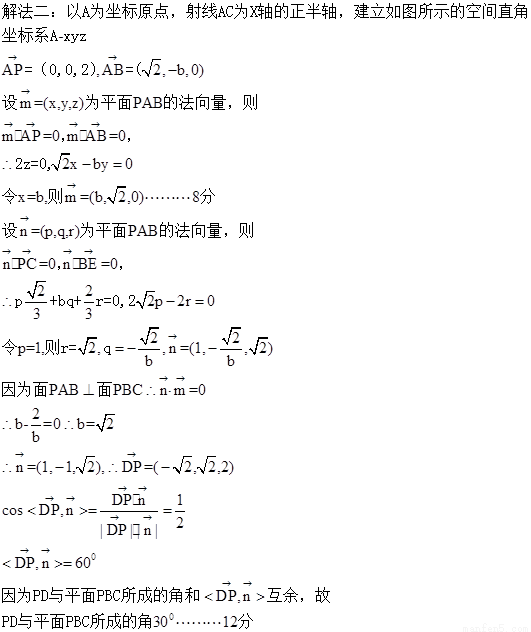
【点评】试题从命题的角度来看,整体上题目与我们平时练习的试题和相似,底面也是特殊的菱形,一个侧面垂直于底面的四棱锥问题,那么创新的地方就是点E的位置的选择是一般的三等分点,这样的解决对于学生来说就是比较有点难度的,因此最好使用空间直角坐标系解决该问题为好。
通过对大学生手机消费情况的调查,探讨影响当代大学生购买手机决策的因素.研究者通过随机抽样对北师大、北大两地共150名被测试者进行了调查,其中男生占45.2%,女生占54.8%.请自愿的被测试者填写自制手机调查问卷(本问卷主要涵盖三方面内容:手机本身因素,服务及购买物理环境因素,广告及品牌效应因素.题目共16道,并随机排序,其中无关题1道).同时,研究人员还在区内各大手机专卖店收集相关资料.本研究一共发放问卷150份,有效回收率为90%.对问卷原始数据大致归类后,再对部分题目进行分析.
在手机本身特点上被测试者选择结果(见表一)
表一 被测试者对手机质量的选择
| 次数 | 百分比 | 有效百分 | 累积百分 | |
有效的 | 持久耐用 | 23 | 15.5 | 16.8 | 16.8 |
信号灵敏 | 54 | 36.5 | 39.4 | 56.2 | |
实用省电 | 12 | 8.1 | 8.8 | 65.0 | |
功能齐全 | 47 | 31.8 | 34.3 | 99.3 | |
其他 | 1 | 0.7 | 0.7 | 100.0 | |
总和 | 137 | 92.6 | 100.0 |
| |
遗漏值 | 系统界定的遗漏值 | 11 | 7.4 |
|
|
总和 |
| 148 | 100.0 |
|
|
在品牌、广告问题上被试关注(结果见表二)
表二 被测试者对广告中认为最可信的因素的选择结果
| 次数 | 百分比 | 有效百分 | 累积百分 | |
有效的 | 专业人士 | 43 | 29.1 | 29.5 | 29.5 |
名人 | 9 | 6.1 | 6.2 | 35.6 | |
统计数据 | 69 | 46.6 | 47.3 | 82.9 | |
其他 | 25 | 16.9 | 17.1 | 100.0 | |
总和 | 146 | 98.6 | 100.0 |
| |
遗漏值 | 系统界定的遗漏值 | 2 | 14 |
|
|
总和 |
| 148 | 100.0 |
|
|

被测试者对最有效的品牌公司形象塑造的策略的选择对以上所搜集的数据以表格或图表分类,在此研究基础上试表述对所搜集的数据处理的结果.并分析潜在因素对大学生购买决策的影响,试从心理特点加以阐释.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com