
题目列表(包括答案和解析)
设f(x)=x2+bx+c,且f(-1)=f(3),则 ( )
A.f(1)>c>f(-1) B.f(1)<c<f(-1)
C.f(1)>f(-1)>c D.f(1)<f(-1)<c
对于解方程x2-2x-3=0的下列步骤:
①设f(x)=x2-2x-3
②计算方程的判别式Δ=22+4×3=16>0
③作f(x)的图象
④将a=1,b=-2,c=-3代入求根公式
x=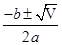 ,得x1=3,x2=-1.
,得x1=3,x2=-1.
其中可作为解方程的算法的有效步骤为( )
A.①② B.②③
C.②④ D.③④
设f(x)=x2-2ax+2.当x∈[-1,+∞)时,f(x)≥a恒成立,求实数a的取值范围.
设f(x)=![]() x2-bx+c,不等式f(x)<0的解集是(-1,3),若f(7+|t|)>f(1+t2),则实数t的取值范围是
x2-bx+c,不等式f(x)<0的解集是(-1,3),若f(7+|t|)>f(1+t2),则实数t的取值范围是
A.(-1,2)
B.(-3,3)
C.(2,3)
D.(-1,3)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com