若二次函数y＝ax²＋bx＋c的图象与x轴交于A(－2，0)，B(4，0)，且函数的最大值为9，则这个二次函数的表达式是________．

若二次函数y＝ax²＋bx＋c的图象与x轴交于A(－2,0)，B(4,0)两点，且函数的最大值为9，则这个二次函数的表达式是________________．

若x₁、x₂是关于一元二次方程ax²＋bx＋c(a≠0)的两个根，则方程的两个根x₁、x₂和系数a、b、c有如下关系：x₁＋x₂＝－，x₁•x₂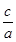＝．把它称为一元二次方程根与系数关系定理．如果设二次函数y＝ax²＋bx＋c(a≠0)的图象与x轴的两个交点为A(x₁，0)，B(x₂，0)．利用根与系数关系定理可以得到A、B连个交点间的距离为：

AB＝|x₁－x₂|＝＝＝＝．

参考以上定理和结论，解答下列问题：

设二次函数y＝ax²＋bx＋c(a＞0)的图象与x轴的两个交点A(x₁，0)、B(x₂，0)，抛物线的顶点为C，显然△ABC为等腰三角形．

(1)当△ABC为直角三角形时，求b²－4ac的值；

(2)当△ABC为等边三角形时，求b²－4ac的值．