
题目列表(包括答案和解析)
解:因为有负根,所以![]() 在y轴左侧有交点,因此
在y轴左侧有交点,因此![]()
解:因为函数没有零点,所以方程![]() 无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
13.证明:(1)令x=y=1,由已知可得f(1)=f(1×1)=f(1)f(1),所以f(1)=1或f(1)=0
若f(1)=0,f(0)=f(1×0)=f(1)f(0)=0,所以f(1)=f(0)与已知条件“![]() ”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
(2)因为f(1)=f[(-1)×(-1)]=f2(-1)=,所以f(-1)=±1,但若f(-1)=1,则f(-1)=f(1)与已知矛盾所以f(-1)不能等于1,只能等于-1。所以任x∈R,f(-x)=f(-1)f(x)=-f(x),因此函数是奇函数
数字1,2,3,4恰好排成一排,如果数字i(i=1,2,3,4)恰好出现在第i个位置上则称有一个巧合,求巧合数![]() 的分布列。
的分布列。
解:因为有负根,所以![]() 在y轴左侧有交点,因此
在y轴左侧有交点,因此![]()
某种产品的广告支出x与销售额y(单位:百万元)之间有如下的对应关系
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
(1)假定x与y之间具有线性相关关系,求回归直线方程.
(2)若实际销售额不少于60百万元,则广告支出应该不少于多少?
在等差数列{an}中,a1=3,其前n项和为Sn,等比数列{bn}的各项均为正数,b1=1,公比为q,且b2+ S2=12,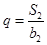 .(Ⅰ)求an 与bn;(Ⅱ)设数列{cn}满足
.(Ⅰ)求an 与bn;(Ⅱ)设数列{cn}满足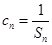 ,求{cn}的前n项和Tn.
,求{cn}的前n项和Tn.
【解析】本试题主要是考查了等比数列的通项公式和求和的运用。第一问中,利用等比数列{bn}的各项均为正数,b1=1,公比为q,且b2+ S2=12,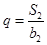 ,可得
,可得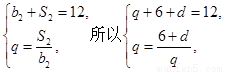 ,解得q=3或q=-4(舍),d=3.得到通项公式故an=3+3(n-1)=3n, bn=3 n-1. 第二问中,
,解得q=3或q=-4(舍),d=3.得到通项公式故an=3+3(n-1)=3n, bn=3 n-1. 第二问中,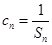 ,由第一问中知道
,由第一问中知道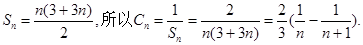 ,然后利用裂项求和得到Tn.
,然后利用裂项求和得到Tn.
解: (Ⅰ) 设:{an}的公差为d,
因为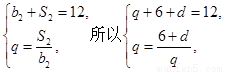 解得q=3或q=-4(舍),d=3.
解得q=3或q=-4(舍),d=3.
故an=3+3(n-1)=3n, bn=3 n-1. ………6分
(Ⅱ)因为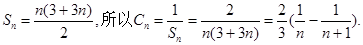 ……………8分
……………8分
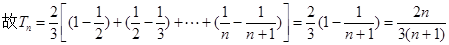
已知二次函数 的二次项系数为
的二次项系数为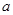 ,且不等式
,且不等式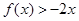 的解集为
的解集为 ,
,
(1)若方程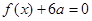 有两个相等的根,求
有两个相等的根,求 的解析式;
的解析式;
(2)若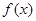 的最大值为正数,求
的最大值为正数,求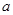 的取值范围.
的取值范围.
【解析】第一问中利用∵f(x)+2x>0的解集为(1,3),
设出二次函数的解析式,然后利用判别式得到a的值。
第二问中,
解:(1)∵f(x)+2x>0的解集为(1,3),
 ①
①
由方程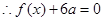
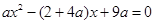 ②
②
∵方程②有两个相等的根,
∴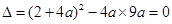 ,
,
即5a2-4a-1=0,解得a=1(舍) 或 a=-1/5
a=-1/5代入①得: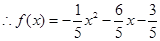
(2)由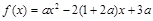
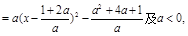
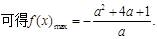
由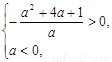 解得:
解得:
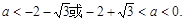
故当f(x)的最大值为正数时,实数a的取值范围是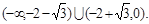
| 3+a | 5-a |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com