练习册

  • 练习册
  • 试题
    ∴ 在AB上存在点F满足条件.此时.AF=．-------12分 【查看更多】

     

    题目列表(包括答案和解析)

    如图，BC是东西方向长为2km的公路，现考虑在点C的正北  方向的点A处建一仓库，设AC=xkm，并在AB上选择一点F，在△ABC内建造边长为ykm的正方形中转站EFGH，其中边HG在公路BC上，且AE=AC．
    （1）求y关于x的函数解析式；
    （2）求正方形中转站EFGH面积的最大值及此时x的值．

    查看答案和解析>>

    若椭圆的中心为原点O，右焦点为F，右准线为l，若在l上存在点M，使线段OM的垂直平分线经过F，则椭圆离心率的取值范围为
    [
    		2
    2
    ，1)
    [
    		2
    2
    ，1)
    ．

    查看答案和解析>>

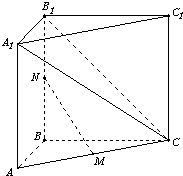    如图，在直三棱柱ABC-A1B1C1中，AA1=BC=AB=2，AB⊥BC．M、N分别是AC和BB1的中点．
    （1）求二面角B1-A1C-C1的大小．
    （2）证明：在AB上存在一个点Q，使得平面QMN⊥平面A1B1C，并求出BQ的长度．

    查看答案和解析>>

    椭圆
    x2
    a2
    +
    y2
    b2
    =1(a＞b＞0)    的右焦点F，直线x=
    a2
    c
    与x轴的交点为A，在椭圆上存在点P满足线段AP的垂直平分线过点F，则椭圆离心率的取值范围是（　　）
    A、(0，
    		2
    2
    ]
    B、(0，
    1
    2
    ]
    C、[
    		2
    -1，1)
    D、[
    1
    2
    ，1)

    查看答案和解析>>

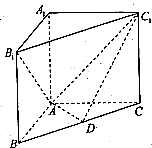    精英家教网三棱柱ABC-A1B1C1中，侧棱AA1⊥底面ABC，AB=AC=2a，AA1=t•a（t＞0，t∈R），∠BAC=120°，
    （1）若在BC上存在点D，使DA1⊥平面AB1C1，求实数t的值，并判断D点的位置；
    （2）在（1）成立的条件下，求二面角D-AC1-B1大小的余弦值．

    查看答案和解析>>


    同步练习册答案