
题目列表(包括答案和解析)
| |EF| | d |
 (2005•静安区一模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=(
(2005•静安区一模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=(| 1 | 2 |
(2010湖北文数)10.记实数![]() …
…![]() 中的最大数为
中的最大数为![]() {
{![]() …
…![]() },最小数为min{
},最小数为min{![]() …
…![]() }.已知
}.已知![]() 的三边边长为
的三边边长为![]() 、
、![]() 、
、![]() (
(![]() ),定义它的倾斜度为
),定义它的倾斜度为
![]()
则“t=1”是“![]() 为等边三解形”的
为等边三解形”的
A,充分布不必要的条件 B.必要而不充分的条件
C.充要条件 D.既不充分也不必要的条件
(2010湖北文数)10.记实数![]() …
…![]() 中的最大数为
中的最大数为![]() {
{![]() …
…![]() },最小数为min{
},最小数为min{![]() …
…![]() }.已知
}.已知![]() 的三边边长为
的三边边长为![]() 、
、![]() 、
、![]() (
(![]() ),定义它的倾斜度为
),定义它的倾斜度为
![]()
则“t=1”是“![]() 为等边三解形”的
为等边三解形”的
A,充分布不必要的条件 B.必要而不充分的条件
C.充要条件 D.既不充分也不必要的条件
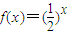 的图象分别交于点An与Bn(如图所示),记Bn的坐标为(an,bn),直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2,一般地记直角梯形AnAn+1Bn+1Bn的面积为sn.
的图象分别交于点An与Bn(如图所示),记Bn的坐标为(an,bn),直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2,一般地记直角梯形AnAn+1Bn+1Bn的面积为sn.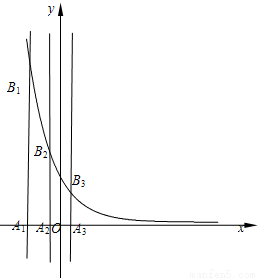
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com